题目内容
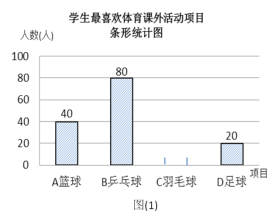
【题目】为了解某校九年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行统计,结果如下表,并绘制了如下尚不完整的统计图,已知![]() ,
,![]() 两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
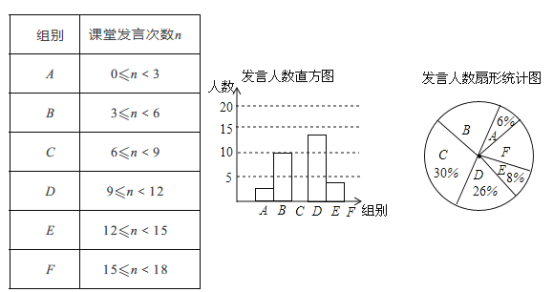
(1)本次抽样的学生人数为_________;
(2)补全条形统计图;
(3)该年级共有学生500人,请估计这天全年级发言次数不少于12的人数;
(4)已知![]() 组发言的学生中有1位女生,
组发言的学生中有1位女生,![]() 组发言的学生中有2位男生,现从
组发言的学生中有2位男生,现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
【答案】(1)50;(2)补全图形见解析;(3)90人;(4)![]() .
.
【解析】
(1)求得B组所占的百分比,然后根据B组有10人即可求得总人数,即样本容量,
(2)求得C、F组的人数,从而补全直方图;
(3)利用总人数乘以对应的百分比即可求解;
(4)分别求出A、E两组的人数,确定出各组的男女生人数,然后列表或画树状图,再根据概率公式计算即可得解.
(1)∵B、E两组发言人数的比为5:2,E组发言人数占8%,
∴B组发言的人数占20%,
由直方图可知B组人数为10人,
所以,被抽查的学生人数为:10÷20%=50人,
∴本次抽样的学生人数为50人.
(2)F组人数为:50×(1-6%-20%-30%-26%-8%)
=50×(1-90%)
=50×10%,
=5(人),
C组人数为:50×30%=15(人),
E组人数为:50×8%=4人
补全条形统计图如图:

(3)∵发言次数不少于12的人数所占的百分比是
![]() ,
,
∴![]() (人).
(人).
∴这天全年级发言次数不少于12的人数为90人;
(4)∵![]() 组发言的学生有50×6%=3(人),有1位女生,
组发言的学生有50×6%=3(人),有1位女生,
∴![]() 组发言的有2位男生.
组发言的有2位男生.
∵![]() 组发言的学生有
组发言的学生有![]() (人),有2位男生,
(人),有2位男生,
∴![]() 组发言的有2位女生.
组发言的有2位女生.
画树状图如图:

由树状图可知共有12种等可能的结果,
其中所抽到的两位学生恰好是一男一女的结果有6种,
∴![]() (恰好是一男一女)
(恰好是一男一女)![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案