题目内容
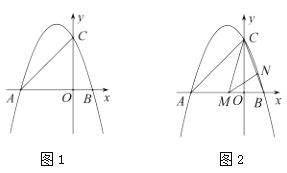
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交x轴、y轴于A,B两点,经过A,B两点的抛物线
分别交x轴、y轴于A,B两点,经过A,B两点的抛物线![]() 与x轴的正半轴相交于点
与x轴的正半轴相交于点![]() .
.

(1)求抛物线的解析式;
(2)若P为线段AB上一点,![]() ,求AP的长;
,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,点N的坐标为(
;(3)存在,点N的坐标为(![]() ,3) 或(
,3) 或(![]() ,
,![]() )
)
【解析】
(1)利用直线![]() 与y轴的交点求得点B的坐标,然后把点B、C的坐标代入
与y轴的交点求得点B的坐标,然后把点B、C的坐标代入![]() ,即可求解;
,即可求解;
(2)先求得点A的坐标,证得△PAO![]() △CAB,利用对应边成比例即可求解;
△CAB,利用对应边成比例即可求解;
(3)分点N在AB的上方或下方两种情况进行讨论,根据平行四边形的性质和等腰直角三角形的性质,利用三角形全等,即可求解.
(1)令![]() ,则
,则![]() ,
,
∴点B的坐标为(0,3),
抛物线![]() 经过点B (0,3),C (1,0),
经过点B (0,3),C (1,0),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)令![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=3,OB=3,OC=1,
![]() ,
,
∵![]() ,且
,且![]() ,
,
∴△PAO![]() △CAB,
△CAB,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
(3)存在,
过点P作PD⊥x轴于点D,
∵OA=3,OB=3,∠AOB=![]() ,
,
∴∠BAO=∠ABO=![]() ,
,
∴△PAD为等腰直角三角形,
∵![]() ,
,
∴PD=AD=2,
∴点P的坐标为(![]() ,2),
,2),
当N在AB的上方时,过点N作NE⊥y轴于点E,如图,
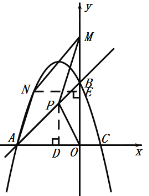
∵四边形APMN为平行四边形,
∴NM∥AP,NM=AP=![]() ,
,
∴∠NME=∠ABO=![]() ,
,
∴△NME为等腰直角三角形,
∴Rt△NME![]() Rt△APD,
Rt△APD,
∴NE=AD=2,
当![]() 时,
时,![]() ,
,
∴点N的坐标为(![]() ,3),
,3),
当N在AB的下方时,过点N作NF⊥y轴于点F,如图,
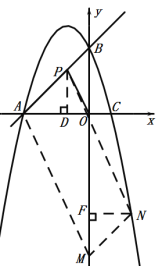
同理可得:Rt△NMF![]() Rt△APD,
Rt△APD,
∴NF=AD=2,
当![]() 时,
时,![]() ,
,
∴点N的坐标为(![]() ,
,![]() ),
),
综上,点N的坐标为(![]() ,3) 或(
,3) 或(![]() ,
,![]() ) .
) .

【题目】合理饮食对学生的身体、智力发育和健康起到了极其重要的作用,只有荤食和素食的合理搭配,才能强化初中生的身体素质,某校为了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:
从七、八年级两个年级中各抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:![]()
八年级:![]()
整理数据:
年级 |
|
|
|
|
七年级 |
|
|
|
|
八年级 |
|
|
|
|
(说明:![]() 为优秀,
为优秀,![]() 为良好,
为良好,![]() 为及格,
为及格,![]() 为不及格)
为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ,
,
(2)比较这两组样本数据的平均数、中位数和众数,你认为哪个年级的体质健康成绩比较好?请说明理由
(3)若七年级共有![]() 名学生,请估计七年级体质健康成绩优秀的学生人数
名学生,请估计七年级体质健康成绩优秀的学生人数