Question

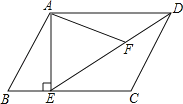
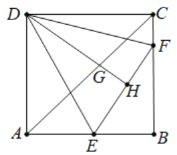
【题目】如图，已知⊙C过菱形ABCD的三个顶点B，A，D，连结BD，过点A作AE∥BD交射线CB于点E．

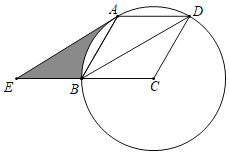
（1）求证：AE是⊙C的切线．

（2）若半径为2，求图中线段AE、线段BE和围成的部分的面积．

（3）在（2）的条件下，在⊙C上取点F，连结AF，使∠DAF＝15°，求点F到直线AD的距离．

Answer 1

【答案】（1）见解析；（2）2﹣π；（3）距离为2﹣或﹣1

【解析】

（1）连接AC．证明AE⊥AC即可解决问题；

（2）证明△ABC是等边三角形，推出∠ACB＝60°，AE＝ACtan60°＝，根据S阴＝S△AEC﹣S扇形ACB求解即可；

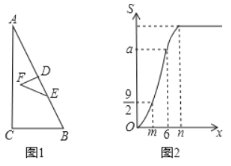
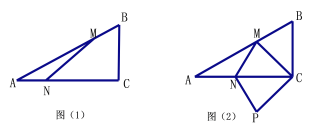
（3）分两种情形：①如图2中，当点F在上时．②如图3中，当点F在优弧上时，分别求解即可．

（1）证明：如图1中，连结AC，

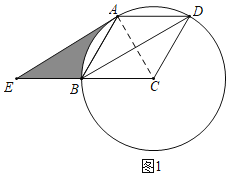
∵四边形ABCD是菱形，

∴AC⊥BD，

又∵BD∥AE，

∴AC⊥AE，

∴AE是⊙O的切线；

（2）如图1中，∵四边形ABCD是菱形，

∴AB＝BC，

又∵AC＝BC，

∴△ABC是等边三角形，

∴∠ACB＝60°，

∵AC＝2，

∴AE＝ACtan60°＝，

∴S阴＝S△AEC﹣S扇形ACB＝×2×﹣＝2﹣π；

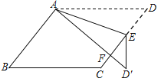
（3）①如图2中，当点F在上时，

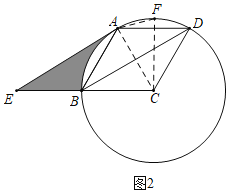
∵∠DAF＝15°，

∴∠DCF＝30°，

∵∠ACD＝60°，

∴∠ACF＝∠FCD，

∴点F是弧AD的中点，

∴CF⊥AD，

∴点F到直线AD的距离＝CF﹣CAcos30°＝2﹣；

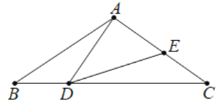
②如图3中，当点F在优弧上时，

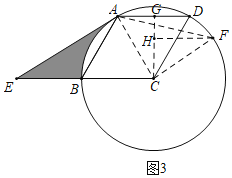
∵∠DAF＝15°，

∴∠DCF＝30°，

过点C作CG⊥AD于D，过点F作FH⊥CG于H，

可得∠AFH＝15°，∠HFC＝30°，

∴CH＝1，

∴点F到直线AD的距离＝CG﹣CH＝ACcos30°﹣CH＝﹣1，

综上所述，满足条件的点F到直线AD的距离为2﹣或﹣1．