题目内容
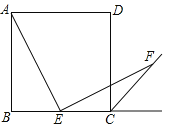
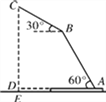
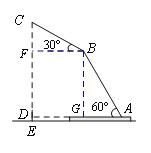
【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:![]() ≈1.732)
≈1.732)

【答案】CE≈51.6cm
【解析】试题分析:要求CE就要考虑直角三角形,所以作辅助线:过点B作BF⊥CD于F,作BG⊥AD于G. 得到两个直角三角形和一个矩形. 这样利用解直角三角形就易求出.
试题解析:如图,过点B作BF⊥CD于F,作BG⊥AD于G..
在Rt△BCF中,∠CBF=30°,∴CF=BC·sin30°=30×![]() =15.
=15.
在Rt△ABG中,∠BAG=60°,∴BG=AB·sin60°=40×![]() =20
=20![]() .
.
∴CE=CF+FD+DE=15+20![]() +2=17+20
+2=17+20![]() ≈51.64≈51.6(cm).
≈51.64≈51.6(cm).
答:此时灯罩顶端C到桌面的高度CE约是51.6cm.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目