Question

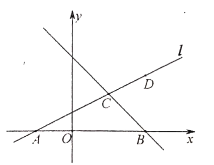
【题目】如图，已知直线过点，.

（1）求直线的解析式；

（2）若直线与轴交于点，且与直线交于点.

①求的面积；

②在直线上是否存在点，使的面积是面积的2倍，如果存在，求出点的坐标；如果不存在，请说明理由.

Answer 1

【答案】（1）；（2）6；（3）或

【解析】

（1）根据点A、D的坐标利用待定系数法即可求出直线l的函数解析式；

（2）令y=-x+4=0求出x值，即可得出点B的坐标，联立两直线解析式成方程组，解方程组即可得出点C的坐标，再根据三角形的面积即可得出结论；

（3）假设存在，设，列出的面积公式求出m，再根据一次函数图象上点的坐标特征即可求出点P的坐标．

解（1）将，，代入

得：解得：

∴直线的解析式为：

（2）联立： ∴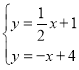

∴

当y=-x+4=0时，x=4

∴

由题意得：

∴

（3）设，由题意得：

∴

∴

∴或

∴或

∴或