��Ŀ����
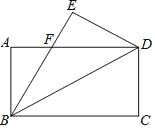
����Ŀ�����꼶�²�̲ĵ�69ҳϰ��14���ı���ABCD�������Σ���E�DZ�BC���е㣬��AEF��90������EF����������ǵ�ƽ����CF�ڵ�F����֤��AE��EF�������Դ����ͬѧ��˵��ӡ�������ѧ�δ���������������������������Ķ�����ͼ���ı���ABCD�������Σ���E�DZ�BC�����ȷֵ㣬��AEF��90������EF����������ǵ�ƽ����CF�ڵ�F����ôAE��EF���������������������֤�����������������˵�����ɣ�
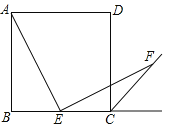
���𰸡����������ɼ�����.
��������
ȡAB�����ȷֵ㣬����GE���ɵ�E�DZ�BC�����ȷֵ㣬�õ�BE=BG�����������ε����ʵõ�AG=EC������ȫ�������ε����ʼ��ɵõ����ۣ�
֤����ȡAB�����ȷֵ㣬����GE��
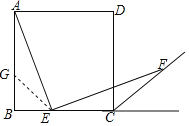
�ߵ�E�DZ�BC�����ȷֵ㣬
��BE=BG��
���ı���ABCD�������Σ�
��AG=EC��
�ߡ�EBGΪ����ֱ�������Σ���֪��AGE=135�㣬
�ߡ�AEF=90�㣬
��BEA+��FEC=90�㣬
��BEA+��BAE=90�㣬
���BAE=��FEC��
���AGE�ա�ECF��ASA����
��AE=EF��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ�������е��ش���̩������ⷿ������½���������ƻ�10���ڽ����������Ⱥ��ס�����⣬ǰ6�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=![]() x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-
x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-![]() x+
x+![]() ��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
z��Ԫ/m2�� | 50 | 52 | 54 | 56 | 58 | �� |
x���꣩ | 1 | 2 | 3 | 4 | 5 | �� |
��1�����z��x�ĺ�����ϵʽ��
��2���������ڵڼ���Ͷ��Ĺ��ⷿ��ȡ�������࣬���Ϊ���ٰ���Ԫ��
��3������6�꿢��Ͷ��ʹ�õĹ��ⷿ�ɽ��20���˵�ס�����⣬�����ƻ��ڵ�10��Ͷ��Ĺ��ⷿ��������������£�Ҫ���˾�ס������ȵ�6���˾�ס��������a%�������ɽ��ס�����������ȵ�6�����1.35a%����a��ֵ��
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
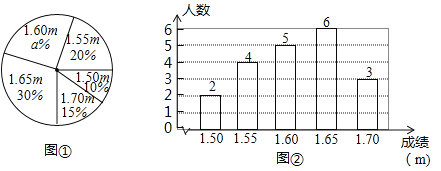
����Ŀ��2017��12�£�����ί���ٸ�У��֯��չ�����������ů���ж���![]() ijУ���꼶������μ�����ξ��������ÿ�����������100��Ϊ���������ļ�����������ʾ������ļ����ø�����ʾ����¼���£�
ijУ���꼶������μ�����ξ��������ÿ�����������100��Ϊ���������ļ�����������ʾ������ļ����ø�����ʾ����¼���£�
�༶ | һ�� | ���� | ���� | �İ� | ��� | ���� |
���� | 40 | 43 | 45 | 44 | 40 | 38 |
���� |
|
|
|
|
|
|
![]() �����������İ�����ٵİ����ټ���
�����������İ�����ٵİ����ټ���
![]() ��У���꼶ѧ�����������ټ������У���꼶ѧ��ƽ��ÿ�˾������ټ����
��У���꼶ѧ�����������ټ������У���꼶ѧ��ƽ��ÿ�˾������ټ����