题目内容
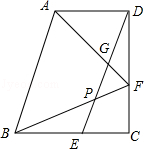
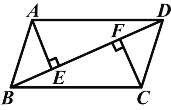
【题目】如图,已知在四边形ABCD中,AE⊥BD于E,CF⊥BD于F,AE=CF,BF=DE.求证:四边形ABCD是平行四边形.
【答案】见解析
【解析】
证明:证法一:∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
又∵AE⊥BD,CF⊥BD.
∴∠AEB=∠CFD=90°.
∵在△ABE和△CDF中,BE=DF,∠AEB=∠CFD,AE=CF,∴△ABE≌△CDF(SAS),∴AB=CD.
∵在△ADE和△CBF中,AE=CF,∠AED=∠BFC=90°,DE=BF,∴△ADE≌△CBF(SAS),∴AD=BC.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
证法二:同证法一,得△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.同理可证:AD∥BC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
证法三:同证法一,得△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,∴AB∥CD.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
证法四:连接AC,交BD于点O.
∵∠AEO=∠CFO=90°,∠AOE=∠COF,AE=CF.
∴△AOE≌△COF(AAS),∴AO=CO,EO=FO.
∵BF=DE,∴BE=DF,∴BE+EO=DF+FO,即BO=DO.
∴四边形ABCD是平行四边形(两条对角线互相平分的四边形是平行四边形).

练习册系列答案
相关题目