��Ŀ����
����Ŀ��һ����������3����ͬ��С��3��С��ֱ��ʾ����1��2��3��ÿ�δӺ��������ȡ��1��С����ȡ��Żأ�Ԥ��ȡ��10�Σ����涨ÿ��ȡ��ʱ��ȡ���ĺ��뼴Ϊ�÷֣���ǰ�˴ε�ȡ��÷�������±���ʾ
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�÷� | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
��1�����1������8��ȡ��÷ֵ�ƽ����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2�����¼�����9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() �������ĸ��ʣ����б�������״ͼ��
�������ĸ��ʣ����б�������״ͼ��
���𰸡���1��2����2���б���������![]()
��������
��1������ƽ�����ļ��㷽�����м��㼴�ɣ�
��2�����б����оٳ����еȿ��ܳ��ֵ�����������ҳ����������������������������ʣ�
��1��![]() ����2+1+1+2+2+3+2+3����8��2��
����2+1+1+2+2+3+2+3����8��2��
��2���ñ����г����п��ܳ��ֵ�������£�
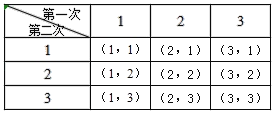
������9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() ��Ҳ�������γ�������ĺ�Ϊ4��
��Ҳ�������γ�������ĺ�Ϊ4��
����9����������к�Ϊ4����3�֣�
��P�����η��ĺ�Ϊ4����![]() ��
��![]() ��
��
���¼�����9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() �������ĸ���Ϊ
�������ĸ���Ϊ![]() ��
��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ