题目内容
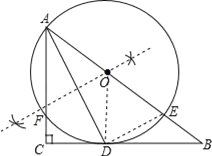
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
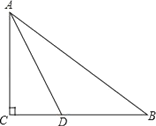
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=2![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
【答案】(1)见解析;(2)见解析;(3)![]() π
π
【解析】
(1)作AD的垂直平分线交AB于点O,以OA为半径画圆O分别交AB、AC于点E、F,则圆O即为所求;
(2)连接OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理可得,OD∥AC,再根据平行线的性质可求证结论;
(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形内角和定理得到∠AOD=120°,根据三角函数的定义得到AE=![]() ,再根据弧长公式可得结论.
,再根据弧长公式可得结论.
(1)解:如图所示,
(2)证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∵BC经过半径OD的外端
∴BC与⊙O相切;
(3)解:连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=∠CAD=30°,
∴∠AOD=120°,
在Rt△ADE中,
AE=![]() =
= ![]() =4,
=4,
∴⊙O的半径=2,
∴劣弧AD的长=![]() =
=![]() π.
π.

【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)