题目内容
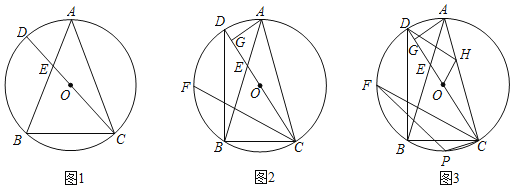
【题目】已知:![]() 内接于⊙
内接于⊙![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,满足
,满足![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() ,
,![]() =
=![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,分别连接
上一点,分别连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交⊙
,交⊙![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)如图1中,连接AD.设∠BEC=3α,∠ACD=α,再根据圆周角定理以及三角形内角和与外角的性质证明∠ACB=∠ABC即可解决问题;
(2)如图2中,连接AD,在CD上取一点Z,使得CZ=BD.证明△ADB≌△AZC(SAS),推出AD=AZ即可解决问题;
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.假设OH=![]() a,PC=2a,求出sin∠OHK=
a,PC=2a,求出sin∠OHK=![]() ,从而得出∠OHK=45°,再根据角度的转化得出∠DAG=∠ACO=∠OAK,从而有tan∠ACD=tan∠DAG=tan∠OAK=
,从而得出∠OHK=45°,再根据角度的转化得出∠DAG=∠ACO=∠OAK,从而有tan∠ACD=tan∠DAG=tan∠OAK=![]() ,进而可求出DG,AG的长,再通过勾股定理以及解直角三角形函数可求出FT,PT的长即可解决问题.
,进而可求出DG,AG的长,再通过勾股定理以及解直角三角形函数可求出FT,PT的长即可解决问题.
(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.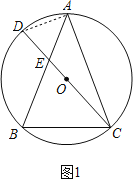
∵∠BEC=∠BAC+∠ACD,
∴∠BAC=2α,
∵CD是直径,
∴∠DAC=90°,
∴∠D=90°-α,
∴∠B=∠D=90°-α,
∵∠ACB=180°-∠BAC-∠ABC=180°-2α-(90°-α)=90°-α.
∴∠ABC=∠ACB,
∴AB=AC.
(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.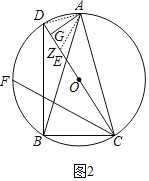
∵![]() =
=![]() ,
,
∴DB=CF,
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴△ADB≌△AZC(SAS),
∴AD=AZ,
∵AG⊥DZ,
∴DG=GZ,
∴CG=CZ+GZ=BD+DG=CF+DG.
(3)解:连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.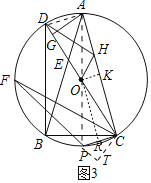
∵CP⊥AC,
∴∠ACP=90°,
∴PA是直径,
∵OR⊥PC,OK⊥AC,
∴PR=RC,∠ORC=∠OKC=∠ACP=90°,
∴四边形OKCR是矩形,
∴RC=OK,
∵OH:PC=1:![]() ,
,
∴可以假设OH=![]() a,PC=2a,
a,PC=2a,
∴PR=RC=a,
∴RC=OK=a,sin∠OHK=![]() ,
,
∴∠OHK=45°.
∵OH⊥DH,
∴∠DHO=90°,
∴∠DHA=180°-90°-45°=45°,
∵CD是直径,
∴∠DAC=90°,
∴∠ADH=90°-45°=45°,
∴∠DHA=∠ADH,
∴AD=AH,
∵∠COP=∠AOD,
∴AD=PC,
∴AH=AD=PC=2a,
∴AK=AH+HK=2a+a=3a,
在Rt△AOK中,tan∠OAK=![]() ,OA=
,OA=![]() ,
,
∴sin∠OAK=![]() ,
,
∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,
∴∠DAG=∠ACD,
∵AO=CO,
∴∠OAK=∠ACO,
∴∠DAG=∠ACO=∠OAK,
∴tan∠ACD=tan∠DAG=tan∠OAK=![]() ,
,
∴AG=3DG,CG=3AG,
∴CG=9DG,
由(2)可知,CG=DG+CF,
∴DG+12=9DG,
∴DG=![]() ,AG=3DG=3×
,AG=3DG=3×![]() =
=![]() ,
,
∴AD=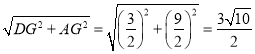 ,
,
∴PC=AD=![]() .
.
∵sin∠F=sin∠OAK,
∴sin∠F=![]() ,
,
∴CT=![]() ,
,
FT=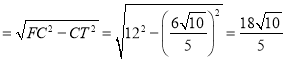 ,
,
PT=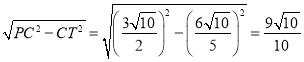 ,
,
∴PF=FT-PT=![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)