Question

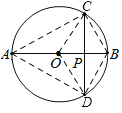
【题目】如图，AB为⊙O的直径，CD是弦，且CD⊥AB于点P，若AB＝4，OP＝1，则弦CD所对的圆周角等于_____度．

Answer 1

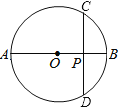
【答案】60或120．

【解析】

先确定弦CD所对的圆周角∠CBD和∠CAD两个，再利用圆的相关性质及菱形的判定证四边形ODBC是菱形，推出,根据圆内接四边形对角互补即可分别求出和的度数．

如图，连接OC，OD，BC，BD，AC，AD，

∵AB为⊙O的直径，AB＝4，

∴OB＝2，

又∵OP＝1，

∴BP＝1，

∵CD⊥AB，

∴CD垂直平分OB，

∴CO＝CB，DO＝DB，

又OC＝OD，

∴OC＝CB＝DB＝OD，

∴四边形ODBC是菱形，

∴∠COD＝∠CBD，

∵∠COD＝2∠CAD，

∴∠CBD＝2∠CAD，

又∵四边形ADBC是圆内接四边形，

∴∠CAD+∠CBD＝180°，

∴∠CAD＝60°，∠CBD＝120°，

∵弦CD所对的圆周角有∠CAD和∠CBD两个，

故答案为：60或120．