Question

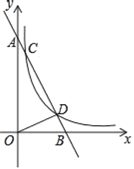
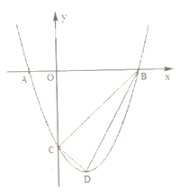
【题目】如图，抛物线与轴交于两点，与轴交于点，设抛物线的顶点为点．

（1）求该抛物线的解析式与顶点的坐标．

（2）试判断的形状，并说明理由．

（3）坐标轴上是否存在点，使得以为顶点的三角形与相似？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1），；（2）是直角三角形，理由见解析；（3）存在，．

【解析】

（1）已知了抛物线图象上的三点坐标，可用待定系数法求出该抛物线的解析式，进而可用配方法或公式法求得顶点D的坐标．

（2）根据B、C、D的坐标，可求得△BCD三边的长，然后判断这三条边的长是否符合勾股定理即可．

（3）假设存在符合条件的P点；首先连接AC，根据A、C的坐标及（2）题所得△BDC三边的比例关系，即可判断出点O符合P点的要求，因此以P、A、C为顶点的三角形也必与△COA相似，那么分别过A、C作线段AC的垂线，这两条垂线与坐标轴的交点也符合点P点要求，可根据相似三角形的性质（或射影定理）求得OP的长，也就得到了点P的坐标．

（1）设抛物线的解析式为．

由抛物线与y轴交于点，可知

即抛物线的解析式为

把代入

解得

∴抛物线的解析式为

∴顶点D的坐标为

（2）是直角三角形．

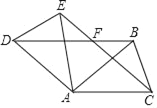
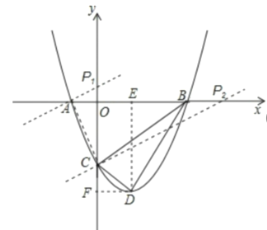
过点D分别作x轴、y轴的垂线，垂足分别为E、F

在中，

∴

在中，

∴

在中，

∴

∴

∴是直角三角形．

（3）连接AC，根据两点的距离公式可得：，则有，可得，得符合条件的点为．

过A作交y轴正半轴于，可知，求得符合条件的点为

过C作交x轴正半轴于，可知，求得符合条件的点为

∴符合条件的点有三个：．