ЬтФПФкШн
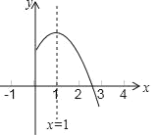
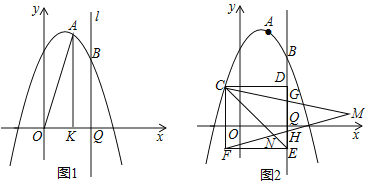
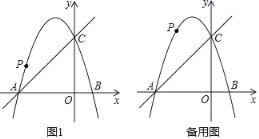
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНЉx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌAЕуЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌBЕудкдЕуЕФзѓВрЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌЕуPЪЧжБЯпBCЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕу
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиCOЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЈШчЭМ1ЫљЪОЃЉЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыДЫЪБЕуPЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌВЂЧѓГіЦфзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3ЃЛЃЈ2ЃЉДцдкЃЎPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈЉ
ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈжБНгНЋBЁЂCСНЕужБНгДњШыyЃНx2+bx+cЧѓНтbЃЌcЕФжЕМДПЩЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉРћгУСтаЮЖдНЧЯпЕФаджЪМАелЕўЕФаджЪПЩвдХаЖЯPЕуЕФзнзјБъЮЊЉ![]() ЃЌСюyЃНЉ
ЃЌСюyЃНЉ![]() МДПЩЕУx2Љ2xЉ3ЃНЉ
МДПЩЕУx2Љ2xЉ3ЃНЉ![]() ЃЌНтИУЗНГЬМДПЩШЗЖЈPЕузјБъЃЛ
ЃЌНтИУЗНГЬМДПЩШЗЖЈPЕузјБъЃЛ
ЃЈ3ЃЉгЩгкЁїABCЕФУцЛ§ЮЊЖЈжЕЃЌЕБЫФБпаЮABCPЕФУцЛ§зюДѓЪБЃЌЁїBPCЕФУцЛ§зюДѓЃЛЙ§PзїyжсЕФЦНааЯпЃЌНЛжБЯпBCгкQЃЌНЛxжсгкFЃЌвзЧѓЕУжБЯпACЕФНтЮіЪНЃЌПЩЩшГіPЕуЕФКсзјБъЃЌШЛКѓИљОнХзЮяЯпКЭжБЯпBCЕФНтЮіЪНЧѓГіQЁЂPЕФзнзјБъЃЌМДПЩЕУЕНPQЕФГЄЃЌвдPQЮЊЕзЃЌBЕуКсзјБъЕФОјЖджЕЮЊИпМДПЩЧѓЕУЁїBPCЕФУцЛ§ЃЌгЩДЫПЩЕУЕНЙигкЫФБпаЮABCPЕФУцЛ§гыPЕуКсзјБъЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪМДПЩЧѓГіЫФБпаЮABCPЕФзюДѓУцЛ§МАЖдгІЕФPЕузјБъЃЎ
ЃЈ1ЃЉЁпCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁрyЃНЉx2+bx+3ЃЌ
АбAЃЈЉ3ЃЌ0ЃЉДњШыЩЯЪНЕУЃЌ0ЃН9Љ3b+3ЃЌ
НтЕУЃЌbЃНЉ2ЃЌ
ЁрИУЖўДЮКЏЪ§НтЮіЪНЮЊЃКyЃНЉx2Љ2x+3ЃЛ
ЃЈ2ЃЉДцдкЃЎШчЭМ1ЃЌ
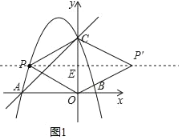
ЩшPЕуЕФзјБъЮЊЃЈxЃЌЉx2Љ2x+3ЃЉЃЌPPЁфНЛCOгкEЃЌ
ЕБЫФБпаЮPOP'CЮЊСтаЮЪБЃЌдђгаPCЃНPOЃЌСЌНгPPЁфЃЌдђPEЁЭCOгкEЃЌ
ЁрOEЃНCEЃН![]() ЃЌ
ЃЌ
СюЉx2Љ2x+3ЃН![]() ЃЌ
ЃЌ
НтЕУЃЌx1ЃНЉ![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЁрPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуPзїyжсЕФЦНааЯпгыBCНЛгкЕуQЃЌгыOAНЛгкЕуFЃЌ
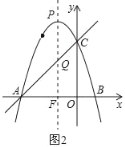
ЩшPЃЈxЃЌЉx2Љ2x+3ЃЉЃЌЩшжБЯпACЕФНтЮіЪНЮЊЃКyЃНkx+tЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊyЃНx+3ЃЌ
дђQЕуЕФзјБъЮЊЃЈxЃЌx+3ЃЉЃЌ
ЕБ0ЃНЉx2Љ2x+3ЃЌ
НтЕУЃКx1ЃН1ЃЌx2ЃНЉ3ЃЌ
ЁрAOЃН3ЃЌOBЃН1ЃЌдђABЃН4ЃЌ
SЫФБпаЮABCPЃНSЁїABC+SЁїAPQ+SЁїCPQ
ЃН![]() ABOC+
ABOC+![]() QPOF+
QPOF+![]() QPAF
QPAF
ЃН![]() ЁС4ЁС3+
ЁС4ЁС3+![]() [ЃЈЉx2Љ2x+3ЃЉЉЃЈx+3ЃЉ]ЁС3
[ЃЈЉx2Љ2x+3ЃЉЉЃЈx+3ЃЉ]ЁС3
ЃНЉ![]() ЃЈx+
ЃЈx+![]() ЃЉ2+
ЃЉ2+![]() ЃЎ
ЃЎ
ЕБxЃНЉ![]() ЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌ
ЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌ
ДЫЪБPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ

 Ек1ОэЕЅдЊдТПМЦкжаЦкФЉЯЕСаД№АИ
Ек1ОэЕЅдЊдТПМЦкжаЦкФЉЯЕСаД№АИ