��Ŀ����
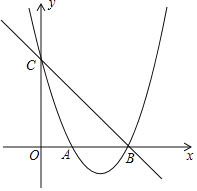
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+4����A����3��0����B��4��0�����㣬����y�ύ�ڵ�C��D��4��4![]() ��0��������P�ӵ�A���������߶�AB��ÿ��1����λ���ȵ��ٶ����B�ƶ���ͬʱ����Q�ӵ�C���������߶�CA��ijһ�ٶ����A�ƶ���
��0��������P�ӵ�A���������߶�AB��ÿ��1����λ���ȵ��ٶ����B�ƶ���ͬʱ����Q�ӵ�C���������߶�CA��ijһ�ٶ����A�ƶ���
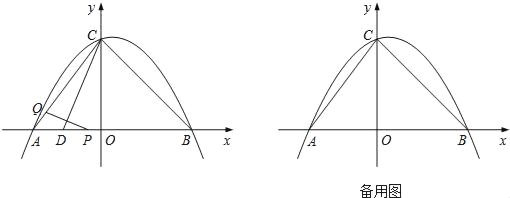
��1����������ߵĽ���ʽ��
��2��������t����ƶ����߶�PQ��CD��ֱƽ�֣����ʱt��ֵ��
��3���ڵ�һ������������ȡһ��G��ʹ��S��GCB��S��GCA���������������ҵ�E�������A��B��C�غϣ���ʹ�á�GBE��45�㣬��E������꣮
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1��ֱ�����ô���ϵ��������κ�������ʽ�ó����ɣ�
��2�����������AQD�ס�ACB����![]() ���ó�DQ��DP�ij��������ó��𰸣�
���ó�DQ��DP�ij��������ó��𰸣�
��3�����ȵó�G�����꣬�����ó���BGM�ס�BEN�����������E�����꣬�������������ε����ʵó�E�����꣮
�⣺��1����A����3��0����B��4��0������y��ax2+bx+4�ã�
![]() ��
��
��ã�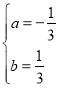 ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2����ͼ������QD��
��B��4��0����D��![]() ��0����
��0����
�ɵ�BD��![]() ��
��
��![]() ��
��
��CO��4��
��BC��4![]() ����BC��BD��
����BC��BD��
���BDC����BCD����QDC��
��DQ��BC��
���AQD�ס�ACB��
��![]() ��
��
��![]() ��
��
��DQ��![]() ��DP��
��DP��
![]() ��
��
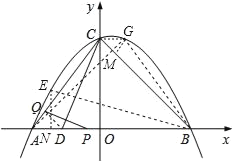
��3����ͼ������G��GM��BC�ڵ�M������E��EN��AB�ڵ�N��
��S��GCB��S��GCA��
��ֻ��CG��ABʱ��G��ŷ������⣬
��C��0��4����
��4����![]() x2+
x2+![]() x+4��
x+4��
��ã�x1��1��x2��0��
��G��1��4����
�ߡ�GBE����OBC��45����
���GBC����ABE��
���BGM�ס�BEN��
��![]() ��
��
��E![]()
��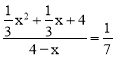
���![]() ��x2��4����ȥ����
��x2��4����ȥ����
��E![]() ��
��

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ���������멁�ɱ�����������ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�