题目内容
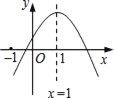
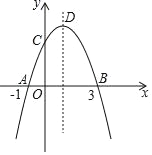
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴为直线x=1,有下列四个判断:
①关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=﹣1,x2=3;
②a﹣b+c=0;
③若抛物线上有三个点分别为(﹣2,y1)、(1,y2)、(2,y3),则y1<y2<y3;
④当OC=3时,点P为抛物线对称轴上的一个动点,则△PCA的周长的最小值是![]() ,
,
上述四个判断中正确的 有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
由抛物线与对称轴的交点对①进行判断;由抛物线经过点(-1,0),代入解析式即可对②进行判断;利用抛物线的对称轴对③进行判断;利用抛物线的对称性得到PA=PB,当B、P、C在一条直线上时,PB+PC=BC,此时PA+PC最小,则△PCA的周长最小,根据勾股定理求得AC、BC即可对④进行判断.
∵抛物线y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0),
∴关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=-1,x2=3,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),
∴a-b+c=0,故②正确;
∵抛物线开口向下,对称轴为直线x=![]() =1,抛物线上有三个点分别为(-2,y1)、(1,y2)、(2,y3),
=1,抛物线上有三个点分别为(-2,y1)、(1,y2)、(2,y3),
∴|-2-1|>|2-1|,
∴y1<y3<y2,故③错误;
∵P为抛物线对称轴上的一个动点,
∴点A与点B为抛物线的对称点,
∴PA=PB,
∴PA+PC=PB+PC,
当B、P、C在一条直线上时,PB+PC=BC,
此时PA+PC最小,则△PCA的周长最小,
∵OA=1,OC=3,OB=3
∴AC=![]() ,BC=2
,BC=2![]() ,
,
∴△PCA的周长最小值为![]() +2
+2![]() .故④错误.
.故④错误.
故选:B.

【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;