题目内容
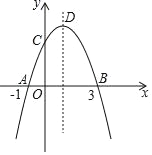
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向移动,以
方向移动,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,连接
,连接![]() ,则下列结论错误的是( )
,则下列结论错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 平分
平分![]()
【答案】D
【解析】
先判断出OA=OB,∠OAB=∠ABO,分两种情况判断出∠OAC=∠BAD,进而判断出△AOC≌△ABD,即可得出结论.
解:∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠ABO=60°
①当点C在线段OB上时,如图1,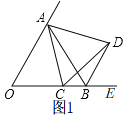
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠CAD-∠CAB=∠OAB-∠CAB,即∠OAC=∠BAD,
在△AOC和△ABD中,
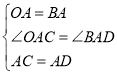 ,
,
∴△AOC≌△ABD,
∴OC=BD,故A正确;
∵△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠∠ABO+∠ABD=120°,故B正确;
∵△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA,故C正确;
∵△AOC≌△ABD,
∴∠OAC=∠BAD,
∴∠OAC+∠CAB>∠BAD,即∠OAB>BAD,AB不平分∠OAD,故D错误.
故选D.
②当点C在OB的延长线上时,如图2,
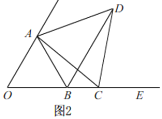
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠CAD+∠CAB=∠OAB+∠CAB,即∠OAC=∠BAD,
在△AOC和△ABD中,
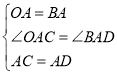 ,
,
∴△AOC≌△ABD,
∴OC=BD,故A正确;
∵△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠ABO+∠ABD=120°,故B正确;
∵△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA,故C正确;
∵△AOC≌△ABD,
∴∠OAC=∠BAD,
∴∠OAC+∠CAB>∠BAD,即∠OAB>BAD,AB不平分∠OAD,故D错误.
故选D.