题目内容
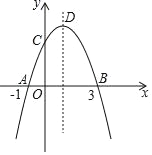
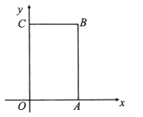
【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为(4，0)，C点的坐标为(0，6)，点B在第一象限内，点P从原点出发，以每秒2个单位的速度沿着O→A→B→C→O的路线移动在点P移动过程中，当P点到x轴的距离为5个单位时，点P移动的时间为________
【答案】
秒或
秒
【解析】
根据点P到x轴的距离为5，可知共有两种情况：P在AB边上或P在OC边上，进行分类讨论，根据点P的运动方向以及距离计算得到点的运动时间即可.
解：根据题意可知，点P距离x轴的距离为5时点P的坐标为（4,5）或（0,5）
当P的坐标为（4,5）时，P在AB边上，运动的距离为4+5=9，所以运动时间为
当P的坐标为（0,5）时，P在OC边上，运动的距离为4+6+4+1=15，所以运动时间为
∴点P的运动时间为或.
故答案为秒或秒
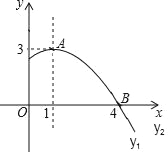
备战中考寒假系列答案
【题目】企业的污水处理有两种方式：一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．1至6月，该企业向污水厂输送的污水量y1（吨）与月份x（1≤x≤6，且x取整数）之间满足的函数关系如下表：
月份x（月） | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量y1（吨） | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
7至12月，该企业自身处理的污水量y2（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为y2=ax2+c（a≠0）．其图象如图所示．1至6月，污水厂处理每吨污水的费用：z1（元）与月份x之间满足函数关系式：z1=
x，该企业自身处理每吨污水的费用：z2（元）与月份x之间满足函数关系式：z2=
x﹣
x2；7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．
（1）请观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y1，y2与x之间的函数关系式；
（2）请你求出该企业去年哪个月用于污水处理的费用W（元）最多，并求出这个最多费用．
