Question

【题目】如图，将一张矩形纸片ABCD折叠，使两个顶点A、C重合，折痕为FG，若AB＝4，BC＝8．

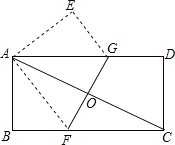
求（1）线段BF的长；

（2）判断△AGF形状并证明；

（3）求线段GF的长．

Answer 1

【答案】（1）BF＝3；（2）△AGF是等腰三角形，理由见解析；（3）GF＝2．

【解析】

（1）根据折叠的性质和垂直平分线的性质求出AF=CF，根据勾股定理得出关于CF的方程，求出CF，得出BF，再根据面积公式求出即可；

（2）由平行线的性质和折叠的性质可证AF=AG，可得△AGF是等腰三角形；

（3）由勾股定理可求AC的长，可求AO的长，由勾股定理可求FO的长，即可得GF的长．

（1）∵将一矩形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG，

∴FG是AC的垂直平分线，

∴AF＝CF，

设AF＝FC＝x，

在Rt△ABF中，由勾股定理得：AB2+BF2＝AF2，

即42+（8﹣x）2＝x2，

解得：x＝5，

即CF＝5，BF＝8﹣5＝3，

（2）△AGF是等腰三角形，

理由如下：∵将一张矩形纸片ABCD折叠，

∴∠AFG＝∠CFG，

∵AD∥BC，

∴∠AGF＝∠CFG

∴∠AGF＝∠AFG，

∴AG＝AF，

∴△AGF是等腰三角形；

（3）∵AB＝4，BC＝8．

∴AC＝ ＝＝4，

∵将一张矩形纸片ABCD折叠，

∴AC⊥GF，

∵AF＝CF，

∴AO＝CO＝2，

∵AF＝AG，AC⊥GF，

∴FO＝GO，

∵FO＝＝＝，

∴GF＝2OF＝2．