题目内容
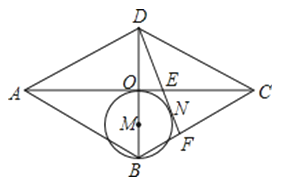
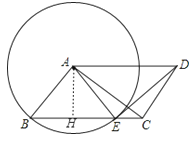
【题目】如图,在ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E.
(1)求证:DE为⊙O的切线;
(2)如果BE=4,CE=2,求DE的值.
【答案】证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,BC=AD,AB∥CD,∠B=∠ADC,
∵AB⊥AC,
∴AC⊥CD,
∴∠ACD=90°,
∵AD∥BC,
∴∠AEB=∠DAE,
∵AB=AE,
∴∠B=∠AEB,AE=DC,
∴∠DAE=∠ADC,
在△AED和△DCA中,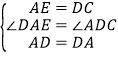 ,
,
∴△AED≌△DCA(SAS),
∴∠AED=∠DCA=90°,
∴AE⊥DE,
∴DE为⊙O的切线;
(2)解:作AH⊥BE,如图,
则BH=CH=![]() BE=2,
BE=2,
∵∠ABH=∠CBA,
∴Rt△BAH∽Rt△BCA,
∴![]() ,即
,即![]() ,
,
∴AB=![]() ,
,
∴AE=![]() ,
,
在Rt△AED中,∵AD=BC=6,AE=![]() ,
,
∴DE=![]() =
=![]() .
.
【解析】(1)根据平行四边形的性质得AB=CD,BC=AD,AB∥CD,∠B=∠ADC,由AB⊥AC得到AC⊥CD,由AD∥BC得到∠AEB=∠DAE,而AB=AE,所以∠B=∠AEB,AE=DC,∠DAE=∠ADC,于是可证明△AED≌△DCA,得到∠AED=∠DCA=90°,则可根据切线的判定定理得到DE为⊙O的切线;
(2)作AH⊥BE,如图,根据垂径定理得BH=CH=![]() BE=2,再证明Rt△BAH∽Rt△BCA,利用相似比计算出AB=2
BE=2,再证明Rt△BAH∽Rt△BCA,利用相似比计算出AB=2![]() , 然后在Rt△AED中利用勾股定理计算DE的长.
, 然后在Rt△AED中利用勾股定理计算DE的长.
【考点精析】通过灵活运用平行四边形的性质和切线的判定定理,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目