题目内容
【题目】如图，已知抛物线y=ax2﹣2ax﹣b（a＞0）与x轴的一个交点为B（﹣1，0），与y轴的负半轴交于点C，顶点为D．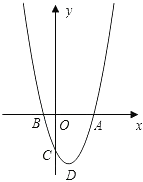
（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点A的坐标；
（2）以AD为直径的圆经过点C．
①求抛物线的解析式；
②点E在抛物线的对称轴上，点F在抛物线上，且以B，A，F，E四点为顶点的四边形为平行四边形，求点F的坐标．
【答案】
（1）
解：对称轴是直线：x=1，
点A的坐标是（3，0）
（2）
解：①如图，连接AC、AD，过D作DM⊥y轴于点M，
解法一：利用△AOC∽△CMD，
在y=ax2﹣2ax﹣b（a＞0）中，当x=1时，y=﹣a﹣b，则D的坐标是（1，﹣a﹣b）．
∵点A、D、C的坐标分别是A（3，0），D（1，﹣a﹣b）、
C（0，﹣b），
∴AO=3，MD=1．
由 
，
得 
，
∴3﹣ab=0．
又∵0=a（﹣1）2﹣2a（﹣1）﹣b，
∴由 
，
得 
，
∴函数解析式为：y=x2﹣2x﹣3．
解法二：利用以AD为直径的圆经过点C，
∵点A、D的坐标分别是A（3，0）、D（1，﹣a﹣b）、C（0，﹣b），
∴AC= 
，CD= 
，AD= 
∵AC2+CD2=AD2
∴3﹣ab=0①
又∵0=a（﹣1）2﹣2a（﹣1）﹣b②
由①、②得a=1，b=3
∴函数解析式为：y=x2﹣2x﹣3．
②F点存在．
如图所示，当四边形BAFE为平行四边形时
则BA∥EF，并且BA=EF．
∵BA=4，
∴EF=4
由于对称轴为x=1，
∴点F的横坐标为5．
将x=5代入y=x2﹣2x﹣3得y=12，∴F（5，12）．
根据抛物线的对称性可知，在对称轴的左侧抛物线上也存在点F，
使得四边形BAEF是平行四边形，此时点F坐标为（﹣3，12）．
当四边形BEAF是平行四边形时，点F即为点D，
此时点F的坐标为（1，﹣4）．
综上所述，点F的坐标为（5，12），（﹣3，12）或（1，﹣4）．
【解析】（1）已知抛物线解析式和点B的坐标求出a值，利用对称轴x=﹣ 
求出对称轴以及点A的坐标．（2）①本题要靠辅助线的帮助．连接AC，AD，过DM⊥y轴于点M．证明△AOC∽△CMD后可推出a，b的值．②证明四边形BAFE为平行四边形，求出BA，EF得出点F的坐标．
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
