题目内容
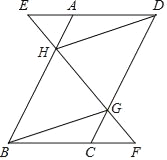
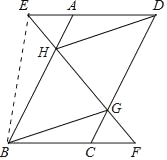
【题目】已知:如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点H,G,连接DH,BG.
(1)求证:△AEH≌△CFG;
(2)连接BE,若BE=DE,则四边形BGDH是什么特殊四边形?请说明理由.
【答案】(1)证明见解析(2)证明见解析
【解析】分析: (1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAH=∠FCG,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BH∥DG,BH=DG,则由有一组对边平行且相等的四边形是平行四边形证明四边形BHDG是平行四边形,再证明BH=DH即可得到四边形BHDG是菱形
详解:
(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAH=∠FCG,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEH与△CFG中,
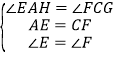 ,
,
∴△AEH≌△CFG(ASA);
(2)连接BE,∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD,
又由(1)得AH=CG,∠AEH=∠F,AE=CF,
∴BH∥DG,BH=DG,,
∴四边形BHDG是平行四边形,
∵AE=CF,AD=BC,
∴DE=BF,
∵BE=DE,
∴BE=BF,
∴∠BEF=∠F,
∵∠AEH=∠F,
∴∠BEF=∠DEF,
在△BEH和△DEH中,
∵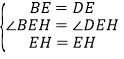 ,
,
∴BH=DH,
∵四边形BHDG是平行四边形,
∴四边形BHDG是菱形.
点睛: 本题主要考查了平行四边形的性质、菱形的判定以及全等三角形的判定与性质,解题的关键是熟练掌握ASA和SAS证明两个三角形的判定以及菱形的判定定理,此题有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目