题目内容
【题目】如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=![]() AB,证明:OM=
AB,证明:OM=![]() CD.
CD.
【答案】证明:设圆的半径是r,ON=x,则AB=2x,
在直角△CON中,CN=![]() =
=![]() ,
,
∵ON⊥CD,
∴CD=2CN=2![]() ,
,
∵OM⊥AB,
∴AM=![]() AB=x,
AB=x,
在△AOM中,OM=![]() =
=![]() ,
,
∴OM=![]() CD.
CD.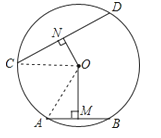
【解析】设圆的半径是r,ON=x,则AB=2x,在直角△CON中利用勾股定理即可求得CN的长,然后根据垂径定理求得CD的长,然后在直角△OAM中,利用勾股定理求得OM的长,即可证得.
【考点精析】根据题目的已知条件,利用垂径定理的相关知识可以得到问题的答案,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目



