题目内容
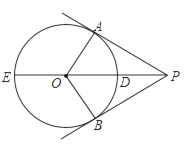
【题目】已知△ABC 中,AD 是∠BAC 的平分线,且 AD=AB,过点 C 作 AD 的垂线,交 AD 的延长线于点 H.
(1)如图 1,若∠BAC=60°.
①直接写出∠B 和∠ACB 的度数;
②若 AB=2,求 AC 和 AH 的长;
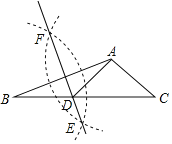
(2)如图 2,用等式表示线段 AH 与 AB+AC 之间的数量关系,并证明.

【答案】(1)①45°,②![]() ;(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.证明见解析.
;(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.证明见解析.
【解析】
(1)①先根据角平分线的定义可得∠BAD=∠CAD=30°,由等腰三角形的性质得∠B=75°,最后利用三角形内角和可得∠ACB=45°;②如图 1,作高线 DE,在 Rt△ADE 中,由∠DAC=30°,AB=AD=2 可得 DE=1,AE=![]() , 在 Rt△CDE 中,由∠ACD=45°,DE=1,可得 EC=1,AC=
, 在 Rt△CDE 中,由∠ACD=45°,DE=1,可得 EC=1,AC= ![]() +1,同理可得 AH 的长;(2)如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH,易证△ACH≌△AFH,则 AC=AF,HC=HF, 根据平行线的性质和等腰三角形的性质可得AG=AH,再由线段的和可得结论.
+1,同理可得 AH 的长;(2)如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH,易证△ACH≌△AFH,则 AC=AF,HC=HF, 根据平行线的性质和等腰三角形的性质可得AG=AH,再由线段的和可得结论.
(1)①∵AD 平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∵AB=AD,
∴∠B=![]() =75°,
=75°,
∴∠ACB=180°﹣60°﹣75°=45°;
②如图 1,过 D 作 DE⊥AC 交 AC 于点 E,
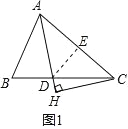
在 Rt△ADE 中,∵∠DAC=30°,AB=AD=2,
∴DE=1,AE=![]() ,
,
在 Rt△CDE 中,∵∠ACD=45°,DE=1,
∴EC=1,
∴AC=![]() +1,
+1,
在 Rt△ACH 中,∵∠DAC=30°,
∴CH=![]() AC=
AC=![]()
∴AH=![]() =
=![]() =
=![]() ;
;
(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.
证明:如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH.
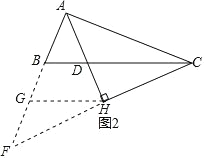
易证△ACH≌△AFH,
∴AC=AF,HC=HF,
∴GH∥BC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠AGH=∠AHG,
∴AG=AH,
∴AB+AC=AB+AF=2AB+BF=2(AB+BG)=2AG=2AH.

 名师点拨卷系列答案
名师点拨卷系列答案