题目内容
【题目】若抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于正半轴C点,且AC=20,BC=15,∠ACB=90°,则此抛物线的解析式为__.
【答案】y=﹣![]() x2+
x2+![]() x+12或y=﹣
x+12或y=﹣![]() x2﹣
x2﹣![]() x+12
x+12
【解析】如图,
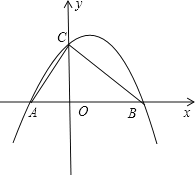
∵∠ACB=90°,AC=20,BC=15,
∴AB=![]() =25,
=25,
∵![]() OCAB=
OCAB=![]() ACBC,
ACBC,
∴OC=![]() =12,
=12,
∴OA=![]() =9,
=9,
∴OB=259=16,
∴抛物线与x轴的交点坐标为(9,0)、(16,0)或(16,0)、(9,0),
当抛物线过点(9,0)、(16,0)时,设抛物线解析式为y=a(x+9)(x16),把C(0,12)代入得a9(16)=12,解得a=![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y=![]() (x+9)(x16),
(x+9)(x16),
即y=![]() x2+
x2+![]() x+12;
x+12;
当抛物线过点(16,0)、(9,0)时,设抛物线解析式为y=a(x+16)(x9),把C(0,12)代入得a16(9)=12,解得a=![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y=![]() (x+16)(x9),
(x+16)(x9),
即y=![]() x2
x2![]() x+12
x+12
综上所述,抛物线解析式为y=![]() x2+
x2+![]() x+12或y=
x+12或y=![]() x2
x2![]() x+12.
x+12.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


