题目内容
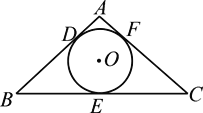
【题目】如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.
(1)求证:△PAO≌△PBO;
(2)已知PA=4,PD=2,求⊙O的半径.
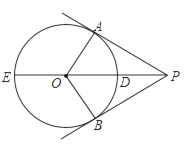
【答案】(1)证明见解析;(2)半径OA的长为3.
【解析】
(1)根据切线长定理得到PA=PB,∠OPA=∠OPB,再根据切线的性质得到∠OAP=∠OBP=90°,然后根据三角形全等的判定方法即可得到结论;
(2)由PA⊙O的切线,得到OA⊥PA,设⊙O的半径为r,则OA=OD=r,在Rt△OAP中根据勾股定理得到r2+42=(r+2)2,然后解方程即可.
(1)∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
在Rt△PAO与Rt△PBO中,![]() ,
,
∴Rt△PAO≌Rt△PBO;
(2)∵PA⊙O的切线,
∴OA⊥PA,
在Rt△OAP中,设⊙O的半径为r,则OP=OD+PD=r+2,
∵OA2+PA2=OP2 ,
∴r2+42=(r+2)2 , 解得r=3,
即半径OA的长为3.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目