题目内容
【题目】已知:正方形 ABCD.
求作:正方形 ABCD 的外接圆.
作法:如图,
(1)分别连接 AC,BD,交于点 O;
(2)以点 O 为圆心,OA 长为半径作⊙O,⊙O 即为所求作的圆.
请回答:该作图的依据是__________________________________.
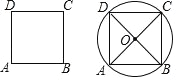
【答案】正方形的对角线相等且互相垂直平分;点到圆心的距离等于圆的半径的点在这个圆上;四边形的四个顶点在同一个圆上,这个圆叫四边形的外接圆.
【解析】
利用正方形的性质得到 OA=OB=OC=OD,则以点O为圆心,OA长为半径作⊙O,点B、C、D都在⊙O 上,从而得到⊙O 为正方形的外接圆.
∵四边形 ABCD 为正方形,
∴OA=OB=OC=OD,
∴⊙O 为正方形的外接圆.
故答案为:正方形的对角线相等且互相垂直平分;点到圆心的距离等于圆的半径的点在这个圆上;四边形的四个顶点在同一个圆上,这个圆叫四边形的外接圆.

练习册系列答案
相关题目