题目内容
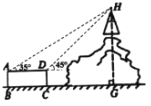
【题目】如图，山上有一座高塔，山脚下有一圆柱形建筑物平台，高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上，在点A处测得塔顶H的仰角为35°，在点D处测得塔顶H的仰角为45°，又测得圆柱形建筑物的上底面直径AD为6m，高CD为2.8m，则塔顶端H到地面的高度HG为（ ）
（参考数据：
，
，
，
）
A.10.8mB.14mC.16.8mD.29.8m
【答案】C
【解析】
延长AD交HG于M，则MG=28m，设DM=x，根据三角函数的概念用含x的代数式表示HM，根据题意列出方程，解方程即可．
延长AD交HG于M，则MG=CD=28m，
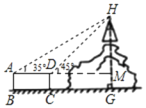
设DM=x，
在Rt△AHM中，HM=（x+6）tan35°，
在Rt△DHM中，HM=xtan45°=x，
∴（x+6）tan35°=x，
即（x+6）×0.70=x，
∴x=14，
即HM=14．
∴HG=14+2.8=16.8（m）．
故选C．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】某商场设立了一个可以自由转动的转盘,并规定：顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据：
(1)计算并完成表格：
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的频率m/n | 0.68 | 0.74 | △ | 0.69 | 0.705 | △ |
(2)请估计，当n很大时，频率将会接近多少?
(3)假如你去转动该转盘一次，你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)
