题目内容
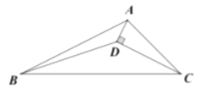
【题目】如图,点![]() 为
为![]() 内部的一点,连接
内部的一点,连接![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
延长AD交BC于F,过B作BE⊥AD于E,得到△BDE是等腰直角三角形,则![]() ,然后证明△BEF≌△CDF,得到BF=CF,EF=DF;延长DA到G,使得AG=BA,然后利用三角形函数的关系,得到边的关系,利用勾股定理构造方程,求出DE的长度,然后求出CF,即可得到BC的长度.
,然后证明△BEF≌△CDF,得到BF=CF,EF=DF;延长DA到G,使得AG=BA,然后利用三角形函数的关系,得到边的关系,利用勾股定理构造方程,求出DE的长度,然后求出CF,即可得到BC的长度.
解:如图,延长AD交BC于F,过B作BE⊥AD于E,
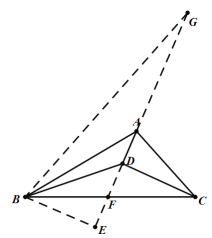
∵AD⊥CD,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△BDE是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵∠BEF=∠CDF=90°,∠BFE=∠CFD,
∴△BEF≌△CDF,
∴BF=CF,EF=DF;
设![]() ,则EF=DF=
,则EF=DF=![]() ,
,![]() ,
,
∵∠ABD+∠BAE=∠BDE=45°,∠ABD+2∠ACD=45°,
∴∠BAE=2∠ACD.
在Rt△ADC中,tan∠ACD=![]() ,
,
在Rt△ABE中,tan∠BAE=![]() ;
;
延长DA到G,使得AG=BA,
∴∠G=∠ABG=![]() ,
,
∴∠G=∠ACD,
在Rt△BEG中,tan∠G=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
在Rt△ABE中,由勾股定理,得:![]() ,
,
即![]() ,
,
整理得:![]() ,
,
∴![]() ,
,![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,
,
即DE=CD=3,
∴EF=DF=![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目