Question

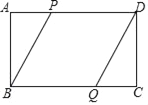
【题目】如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ．

（1）求证：BP=DQ；

（2）若AB=4，且当PD=5时四边形PBQD为菱形．求AD为多少．

Answer 1

【答案】（1）见解析；（2）8.

【解析】

（1）依据矩形的性质，通过全等三角形的判定定理判定△ABP≌△QCD，所以BP=DQ．

（2）设AP=a，AD=5+a．当四边形PBQD是菱形时，PB=PD=5．在直角△ABP中，根据勾股定理得到AP2+AB2=PB2，即a2+42=52，由此可以求得a，再可得AD的长度．

证明：（1）∵四边形ABCD是矩形，

∴∠A=∠C=90°，AB=CD，

在Rt△ABP和Rt△QCD中，

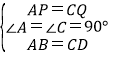
∴△ABP≌△QCD（ASA），

∴BP=DQ；

（2）设AP=a，AD=5+a．

当四边形PBQD是菱形时，PB=PD=5，

在直角△ABP中，根据勾股定理得到AP2+AB2=PB2，即a2+42=52，

可得：a=3，

所以AD=3+5=8．