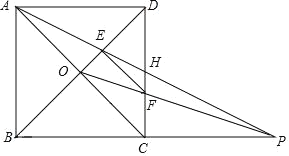
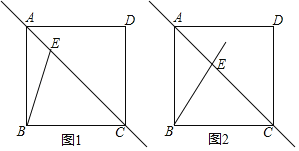
题目内容
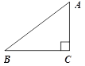
【题目】如图，一张三角形纸片ABC，其中∠C = 90°，AC = 6，BC = 8．如果小明同学将纸片做了两次折叠．第一次使点A落在C处，在纸片上的折痕长记为m；然后将纸片展平做第二次折叠，使点A落在B处，在纸片上的折痕长记为n．那么m，n之间的关系是m_____n．（填“＞”，“=”或“＜” ）
【答案】＞
【解析】
由三角形中位线定理求出m=4；由勾股定理求出AB=10，证明△BDF∽△BCA，得出对应边成比例求出DF即可．
如图所示：
由折叠的性质得：DE是线段AC的垂直平分线，
∴DE是△ABC的中位线，
∴m=DE=
BC=4，
∵∠C=90°，AC=6，BC=8，
∴AB=
=10，
由折叠的性质得：AD=BD=AB=5，∠BDF=90°，
∵∠B=∠B，
∴△BDF∽△BCA，
∴
，即
，
解得：DF=
，即n=，
∴m＞n；
故答案为：>．
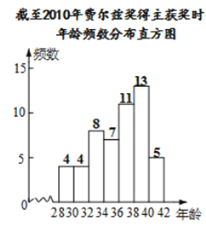
【题目】下面数据是截至2010年费尔兹奖得主获奖时的年龄：
29 39 35 33 39 28 33 35 31 31 37 32 38
36 31 39 32 38 37 34 29 34 38 32 35 36
33 29 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 40 31 38 38 40 40 37
小果、小冻、小甜将数据整理，分别按组距是2，5，10进行分组，列出频数分布表，画出频数分布直方图，如下：
年龄 | 频数 |
| 4 |
| 4 |
| 8 |
| 7 |
| 11 |
| 13 |
| 5 |
年龄 | 频数 |
| 4 |
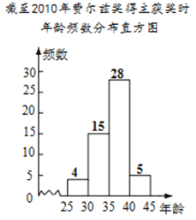
| 15 |
| 28 |
| 5 |
年龄 | 频数 |
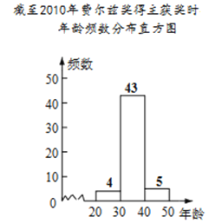
| 4 |
| 43 |
| 5 |
根据以上材料回答问题：
小果、小冻、小甜三人中，比较哪一位同学分组能更好的说明费尔兹奖得主获奖时的年龄分布，并简要说明其他两位同学分组的不足之处．
费尔兹奖是国际上享有崇高声誉的一个数学奖项，每4年评选一次，主要授予年轻的数学家，美籍华人丘成桐（1949年出生）1982年获费尔兹奖．