题目内容
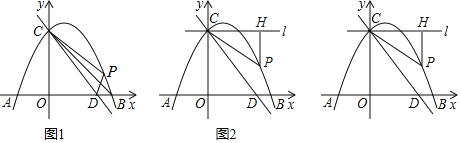
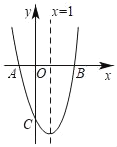
【题目】已知:直线l过点(0,2),且与x轴平行;直线![]() 与y轴交于A点,与直线l交于B点;抛物线
与y轴交于A点,与直线l交于B点;抛物线![]() 的顶点为C.
的顶点为C.
(1)求A,B两点的坐标;
(2)求点C的坐标(用m表示);
(3)若抛物线![]() 与线段AB有公共点,求m的取值范围.
与线段AB有公共点,求m的取值范围.
【答案】(1)A(0,1),B(4,2);(2)C(m,2);(3)![]() .
.
【解析】
(1)根据自变量与函数值得对应关系,可得答案;
(2)根据配方法,可得顶点坐标;
(3)根据图象过线段的端点,可得m的值,结合抛物线的顶点坐标,即可解决问题.
(1)当![]() 时,
时,![]() ,即A点坐标为(0,1);
,即A点坐标为(0,1);
又直线l过点(0,2),且与x轴平行,所以直线l是![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() ,即B(4,2);
,即B(4,2);
(2)配方,得![]() =
=![]() ,
,
所以顶点C的坐标为(m,2);
(3)∵![]() 过A(0,1),
过A(0,1),
∴![]() 或
或![]() .
.
又∵![]() 过B(4,2),
过B(4,2),
∴![]() ,
,
当线段AB与抛物线只有一个交点时,
即方程![]() =
=![]() 有两个相等的实数根,
有两个相等的实数根,
方程整理得![]() =0,
=0,
则有![]() ,解得
,解得![]() ,
,
∵抛物线的顶点为(m,2),观察图象可知,抛物线![]() 与线段AB有公共点,m的取值范围为
与线段AB有公共点,m的取值范围为![]() .
.

【题目】阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况.
饮酒后的时间x(小时) | … |
|
|
| 1 |
|
| 2 | 3 | 4 | 5 | 6 | … |
血液中酒精含量y (毫克/百毫升) | … |
| 150 |
| 200 |
| 150 |
|
|
| 45 |
| … |
下面是小明的探究过程,请补充完整:
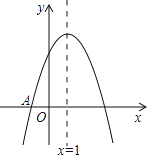
(1)如图,在平面直角坐标系xOy中,以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=![]() 两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.