题目内容
【题目】在平面直角坐标系![]() 中,对于双曲线
中,对于双曲线![]() 和双曲线
和双曲线![]() ,如果
,如果![]() ,则称双曲线
,则称双曲线![]() 和双曲线
和双曲线![]() 为“倍半双曲线”,双曲线
为“倍半双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“倍双曲线”,双曲线
的“倍双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“半双曲线”,
的“半双曲线”,

(1)请你写出双曲线![]() 的“倍双曲线”是_____;双曲线
的“倍双曲线”是_____;双曲线![]() 的“半双曲线”是______;
的“半双曲线”是______;
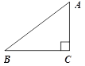
(2)如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,求
,求![]() 的面积;
的面积;
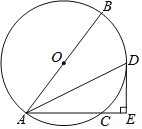
(3)如图2,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,若
,若![]() 的面积记为
的面积记为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的面积为1;(3)
的面积为1;(3)![]() .
.
【解析】
(1)直接利用“倍双曲线”的定义即可;
(2)利用双曲线的性质即可;
(3)先利用双曲线上的点设出![]() 的横坐标,进而表示出
的横坐标,进而表示出![]() 的坐标;
的坐标;
用三角形的面积公式建立不等式即可得出结论;
(1)由“倍双曲线”的定义
∴双曲线![]() ,的“倍双曲线”是
,的“倍双曲线”是![]() ;
;
双曲线![]() 的“半双曲线”是
的“半双曲线”是![]() .
.
故答案为![]() ,
,![]() ;
;
(2)如图1,
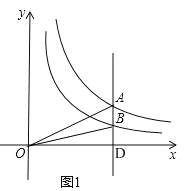
∵双曲线![]() 的“半双曲线”是
的“半双曲线”是![]() ,
,
∴![]() 的面积为2,
的面积为2,![]() 的面积为1,
的面积为1,
∴![]() 的面积为1.
的面积为1.
(3)如图2,
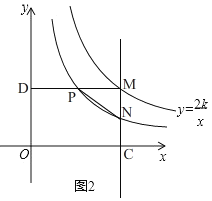
依题意可知双曲线![]() 的“半双曲线”为
的“半双曲线”为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
∴![]() .
.
∴![]() .
.
同理![]() .
.
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() ,
,

【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
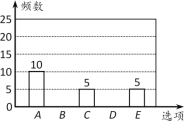
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.