Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ‘ŕ’ż∑Ĺ–ő![]() ÷–£¨Ķ„
÷–£¨Ķ„![]() «∂‘Ĺ«ŌŖ
«∂‘Ĺ«ŌŖ![]() …ŌĶń∂ĮĶ„£®”ŽĶ„
…ŌĶń∂ĮĶ„£®”ŽĶ„![]() ≤Ľ÷ōļŌ£©£¨Ń¨Ĺ”
≤Ľ÷ōļŌ£©£¨Ń¨Ĺ”![]() £ģ
£ģ
£®1£©Ĺę…šŌŖ![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™45°„£¨ĹĽ÷ĪŌŖ
ň≥ Ī’Ž–ż◊™45°„£¨ĹĽ÷ĪŌŖ![]() ”ŕĶ„
”ŕĶ„![]() £ģ
£ģ
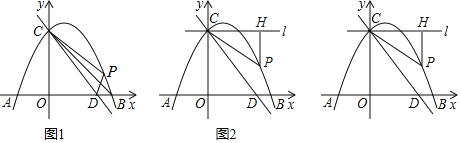
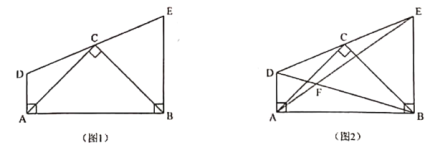
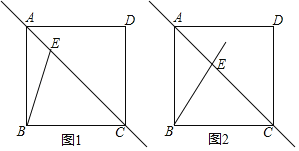
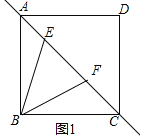
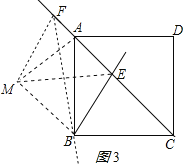
ĘŔ“ņŐ‚“‚≤Ļ»ęÕľ1£Ľ
Ęŕ–°—–Õ®ĻżĻŘ≤ž°Ę Ķ—ť£¨∑ĘŌ÷ŌŖ∂ő![]() £¨
£¨![]() £¨
£¨![]() īś‘ŕ“‘Ō¬ żŃŅĻōŌĶ£ļ
īś‘ŕ“‘Ō¬ żŃŅĻōŌĶ£ļ
![]() ”Ž
”Ž![]() Ķń∆Ĺ∑ĹļÕĶ»”ŕ
Ķń∆Ĺ∑ĹļÕĶ»”ŕ![]() Ķń∆Ĺ∑Ĺ£ģ–°—–į—’‚łŲ≤¬ŌŽ”ŽÕ¨—ß√«ĹÝ––ĹĽŃų£¨Õ®ĻżŐ÷¬Ř£¨–ő≥…÷§√ųł√≤¬ŌŽĶńľł÷÷ŌŽ∑®£ļ
Ķń∆Ĺ∑Ĺ£ģ–°—–į—’‚łŲ≤¬ŌŽ”ŽÕ¨—ß√«ĹÝ––ĹĽŃų£¨Õ®ĻżŐ÷¬Ř£¨–ő≥…÷§√ųł√≤¬ŌŽĶńľł÷÷ŌŽ∑®£ļ
ŌŽ∑®1£ļĹęŌŖ∂ő![]() »∆Ķ„
»∆Ķ„![]() ńś Ī’Ž–ż◊™90°„£¨Ķ√ĶĹŌŖ∂ő
ńś Ī’Ž–ż◊™90°„£¨Ķ√ĶĹŌŖ∂ő![]() £¨“™÷§
£¨“™÷§![]() ĶńĻōŌĶ£¨÷Ľ–Ť÷§
ĶńĻōŌĶ£¨÷Ľ–Ť÷§![]() ĶńĻōŌĶ£ģ
ĶńĻōŌĶ£ģ
ŌŽ∑®2£ļĹę![]() —ō
—ō![]() ∑≠’Ř£¨Ķ√ĶĹ
∑≠’Ř£¨Ķ√ĶĹ![]() £¨“™÷§
£¨“™÷§![]() ĶńĻōŌĶ£¨÷Ľ–Ť÷§
ĶńĻōŌĶ£¨÷Ľ–Ť÷§![]() ĶńĻōŌĶ£ģ
ĶńĻōŌĶ£ģ
°≠
«Žń„≤őŅľ…Ō√śĶńŌŽ∑®£¨”√Ķ» ĹĪŪ ĺŌŖ∂ő![]() Ķń żŃŅĻōŌĶ≤Ę÷§√ų£Ľ£®“Ľ÷÷∑Ĺ∑®ľīŅ…£©
Ķń żŃŅĻōŌĶ≤Ę÷§√ų£Ľ£®“Ľ÷÷∑Ĺ∑®ľīŅ…£©
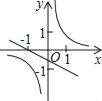
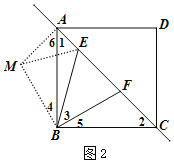
£®2£©»ÁÕľ2£¨»ŰĹę÷ĪŌŖ![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™135°„£¨ĹĽ÷ĪŌŖ
ň≥ Ī’Ž–ż◊™135°„£¨ĹĽ÷ĪŌŖ![]() ”ŕĶ„
”ŕĶ„![]() £ģ–°—–ÕÍ≥…◊ųÕľļů£¨∑ĘŌ÷÷ĪŌŖ
£ģ–°—–ÕÍ≥…◊ųÕľļů£¨∑ĘŌ÷÷ĪŌŖ![]() …Ōīś‘໿ŐűŌŖ∂ő£®≤ĽŐŪľ”ł®÷ķŌŖ£©¬ķ◊„£ļ∆š÷–ŃĹŐűŌŖ∂őĶń∆Ĺ∑ĹļÕĶ»”ŕĶ໿ŐűŌŖ∂őĶń∆Ĺ∑Ĺ£¨«Ž÷ĪĹ””√Ķ» ĹĪŪ ĺ’‚»żŐűŌŖ∂őĶń żŃŅĻōŌĶ£ģ
…Ōīś‘໿ŐűŌŖ∂ő£®≤ĽŐŪľ”ł®÷ķŌŖ£©¬ķ◊„£ļ∆š÷–ŃĹŐűŌŖ∂őĶń∆Ĺ∑ĹļÕĶ»”ŕĶ໿ŐűŌŖ∂őĶń∆Ĺ∑Ĺ£¨«Ž÷ĪĹ””√Ķ» ĹĪŪ ĺ’‚»żŐűŌŖ∂őĶń żŃŅĻōŌĶ£ģ
°ĺīūįł°Ņ£®1£©ĘŔ≤Ļ»ęÕľ–ő£¨»ÁÕľ1ňý ĺ£¨ľŻĹ‚őŲ£ĽĘŕ![]() £ĽņŪ”…ľŻĹ‚őŲ£Ľ£®2£©
£ĽņŪ”…ľŻĹ‚őŲ£Ľ£®2£©![]() £ĽņŪ”…ľŻĹ‚őŲ.
£ĽņŪ”…ľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
£®1£©ĘŔłýĺ›Ő‚“‚≤Ļ»ęÕľ–őľīŅ…£Ľ
ĘŕĻż![]() ◊ų
◊ų![]() £¨ Ļ
£¨ Ļ![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨”…’ż∑Ĺ–őĶń–‘÷ Ķ√≥Ų
£¨”…’ż∑Ĺ–őĶń–‘÷ Ķ√≥Ų![]() £¨
£¨![]() £¨
£¨![]() £¨”…
£¨”…![]() ÷§√ų
÷§√ų![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨÷§≥Ų
£¨÷§≥Ų![]() £¨”…
£¨”…![]() ÷§√ų
÷§√ų![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨÷§≥Ų
£¨÷§≥Ų![]() £¨‘ŕ
£¨‘ŕ![]() ÷–£¨”…ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
÷–£¨”…ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£®2£©Ļż![]() ◊ų
◊ų![]() £¨ Ļ
£¨ Ļ![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨”…
£¨”…![]() ÷§Ķ√£ļ
÷§Ķ√£ļ![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨‘Ŕ”…
£¨‘Ŕ”…![]() ÷§Ķ√£ļ
÷§Ķ√£ļ![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨
£¨![]() £¨÷§≥Ų
£¨÷§≥Ų![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨‘ŕ
£¨‘ŕ![]() ÷–£¨”…ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĹŠ¬Ř£ģ
÷–£¨”…ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĹŠ¬Ř£ģ
Ĺ‚£ļ£®1£©ĘŔ≤Ļ»ęÕľ–ő£¨»ÁÕľ1ňý ĺ£ļ
Ęŕ![]() £ĽņŪ”…»ÁŌ¬£ļ
£ĽņŪ”…»ÁŌ¬£ļ
Ļż![]() ◊ų
◊ų![]() £¨ Ļ
£¨ Ļ![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨»ÁÕľ2ňý ĺ£ļ
£¨»ÁÕľ2ňý ĺ£ļ
°ŖňńĪŖ–ő![]() «’ż∑Ĺ–ő£¨
«’ż∑Ĺ–ő£¨
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨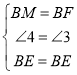 £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨°Ŗ
£¨°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨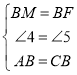 £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ÷–£¨
÷–£¨![]() £¨
£¨
°ŗ![]() £Ľ
£Ľ
£®2£©![]() £ĽņŪ”…»ÁŌ¬£ļ
£ĽņŪ”…»ÁŌ¬£ļ
Ļż![]() ◊ų
◊ų![]() £¨ Ļ
£¨ Ļ![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨
£¨
°Ŗ÷ĪŌŖ![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™135°„£¨ĹĽ÷ĪŌŖ
ň≥ Ī’Ž–ż◊™135°„£¨ĹĽ÷ĪŌŖ![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨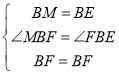 £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨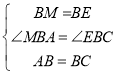 £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
‘ŕ![]() ÷–£¨
÷–£¨![]() £¨
£¨
°ŗ![]() £ģ
£ģ

°ĺŐ‚ńŅ°Ņ2022ńÍĹę‘ŕĪĪĺ©©Ā©Ā’Ňľ“ŅŕĺŔįž∂¨ľĺį¬‘ňĽŠ£¨ĪĪĺ©Ĺę≥…ő™ ņĹÁ…ŌĶŕ“ĽłŲľ»ĺŔįžŌńľĺį¬‘ňĽŠ£¨”÷ĺŔįž∂¨ľĺį¬‘ňĽŠĶń≥« –£¨ń≥–£Ņ™…ŤŃňĪý«Ú—°–řŅő£¨12√ŻÕ¨—ßĪĽ∑÷≥…ľ◊°Ę““ŃĹ◊ťĹÝ––—ĶŃ∑£¨ňŻ√«Ķń…ŪłŖ(Ķ•őĽ£ļcm)»ÁĪŪňý ĺ£ļ
∂”‘Ī1 | ∂”‘Ī1 | ∂”‘Ī1 | ∂”‘Ī1 | ∂”‘Ī1 | ∂”‘Ī1 | |
ľ◊◊ť | 176 | 177 | 175 | 176 | 177 | 175 |
““◊ť | 178 | 175 | 170 | 174 | 183 | 176 |
…ŤŃĹ∂”∂”‘Ī…ŪłŖĶń∆Ĺĺý ż“ņīőő™![]() £¨
£¨![]() £¨∑Ĺ≤Ó“ņīőő™
£¨∑Ĺ≤Ó“ņīőő™![]() £¨
£¨![]() £¨Ō¬Ń–ĻōŌĶ÷–’ż»∑Ķń «( )
£¨Ō¬Ń–ĻōŌĶ÷–’ż»∑Ķń «( )
A.![]() £¨
£¨![]() B.
B.![]() £¨
£¨![]()
C.![]() £¨
£¨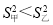 D.
D.![]() £¨
£¨![]()
°ĺŐ‚ńŅ°Ņ‘ń∂ŃŌ¬Ń–≤ńŃŌ£ļ
Ķ—ť żĺ›Ō‘ ĺ£¨“Ľį„≥…»ňļ»250ļŃ…żĶÕ∂»į◊ĺ∆ļů£¨∆š—™“ļ÷–ĺ∆ĺęļ¨ŃŅ(ļŃŅň/įŔļŃ…ż)ňś ĪľšĶń‘Ųľ”÷ū≤Ĺ‘ŲłŖīÔĶĹ∑Ś÷Ķ£¨÷ģļů—™“ļ÷–ĺ∆ĺęļ¨ŃŅňś ĪľšĶń‘Ųľ”÷ūĹ•ĹĶĶÕ£ģ
–°√ųłýĺ›ŌŗĻō żĺ›ļÕ—ßŌįļĮ żĶńĺ≠—ť£¨∂‘—™“ļ÷–ĺ∆ĺęļ¨ŃŅňś ĪľšĪšĽĮĶńĻś¬…ĹÝ––ŃňŐĹĺŅ£¨∑ĘŌ÷—™“ļ÷–ĺ∆ĺęļ¨ŃŅy « ĪľšxĶńļĮ ż£¨∆š÷–yĪŪ ĺ—™“ļ÷–ĺ∆ĺęļ¨ŃŅ(ļŃŅň/įŔļŃ…ż)£¨xĪŪ ĺ“Żĺ∆ļůĶń Īľš(–° Ī)£ģ
Ō¬ĪŪľ«¬ľŃň6–° Īńŕ11łŲ ĪľšĶ„—™“ļ÷–ĺ∆ĺęļ¨ŃŅy(ļŃŅň/įŔļŃ…ż)ňś“Żĺ∆ļůĶń Īľšx(–° Ī)(x£ĺ0)ĶńĪšĽĮ«ťŅŲ£ģ
“Żĺ∆ļůĶń Īľšx(–° Ī) | °≠ |
|
|
| 1 |
|
| 2 | 3 | 4 | 5 | 6 | °≠ |
—™“ļ÷–ĺ∆ĺęļ¨ŃŅy (ļŃŅň/įŔļŃ…ż) | °≠ |
| 150 |
| 200 |
| 150 |
|
|
| 45 |
| °≠ |
Ō¬√ś «–°√ųĶńŐĹĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ’Ż£ļ
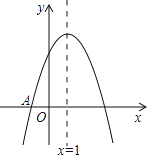
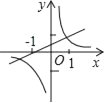
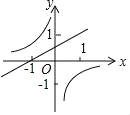
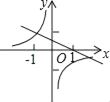
(1)»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨“‘…ŌĪŪ÷–łų∂‘ ż÷Ķő™◊ÝĪÍ√ŤĶ„£¨Õľ÷–“—łÝ≥Ų≤Ņ∑÷Ķ„£¨«Žń„√Ť≥Ų £”ŗĶńĶ„£¨Ľ≠≥Ų—™“ļ÷–ĺ∆ĺęļ¨ŃŅyňś ĪľšxĪšĽĮĶńļĮ żÕľŌů£Ľ
(2)ĻŘ≤žĪŪ÷– żĺ›ľįÕľŌůŅ…∑ĘŌ÷īňļĮ żÕľŌů‘ŕ÷ĪŌŖx£Ĺ![]() ŃĹ≤ŗŅ…“‘”√≤ĽÕ¨ĶńļĮ żĪŪīÔ ĹĪŪ ĺ£¨«Žń„»ő—°∆š÷–“Ľ≤Ņ∑÷–ī≥ŲĪŪīÔ Ĺ£Ľ
ŃĹ≤ŗŅ…“‘”√≤ĽÕ¨ĶńļĮ żĪŪīÔ ĹĪŪ ĺ£¨«Žń„»ő—°∆š÷–“Ľ≤Ņ∑÷–ī≥ŲĪŪīÔ Ĺ£Ľ
(3)įīĻķľ“Ļś∂®£¨≥ĶŃĺľ› Ľ»ň‘Ī—™“ļ÷–Ķńĺ∆ĺęļ¨ŃŅīů”ŕĽÚĶ»”ŕ20ļŃŅň/įŔļŃ…ż Ī Ű”ŕ°įĺ∆ļůľ› Ľ°Ī£¨≤Ľń‹ľ›≥Ķ…Ō¬∑£ģ≤ő’’…Ō Ų ż—ßń£–Õ£¨ľŔ…Ťń≥ľ› Ľ‘ĪÕŪ…Ō20£ļ00‘ŕľ“ļ»ÕÍ250ļŃ…żĶÕ∂»į◊ĺ∆£¨Ķŕ∂ĢŐž‘Á…Ō6£ļ30ń‹∑Ůľ›≥Ķ»•…Ōįŗ£Ņ«ŽňĶ√ųņŪ”…£ģ