题目内容
【题目】已知抛物线y=ax2+bx+2经过A（﹣1，0），B（2，0），C三点．直线y=mx+ 
交抛物线于A，Q两点，点P是抛物线上直线AQ上方的一个动点，作PF⊥x轴，垂足为F，交AQ于点N．
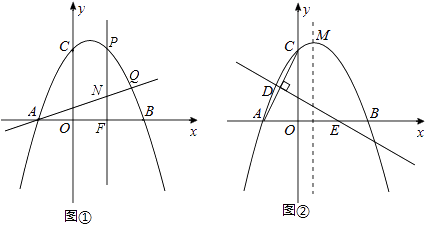
（1）求抛物线的解析式；
（2）如图①，当点P运动到什么位置时，线段PN=2NF，求出此时点P的坐标；
（3）如图②，线段AC的垂直平分线交x轴于点E，垂足为D，点M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵抛物线y=ax2+bx+2经过A（﹣1，0），B（2，0），
∴将点A和点B的坐标代入得： 
，解得a=﹣1，b=1，
∴抛物线的解析式为y=﹣x2+x+2
（2）
解：直线y=mx+ 
交抛物线与A、Q两点，把A（﹣1，0）代入解析式得：m= ，
∴直线AQ的解析式为y= x+ ．
设点P的横坐标为n，则P（n，﹣n2+n+2），N（n， n+ ），F（n，0），
∴PN=﹣n2+n+2﹣（ n+ ）=﹣n2+ n+ 
，NF= n+ ．
∵PN=2NF，即﹣n2+ n+ =2×（ n+ ），解得：n=﹣1或 ．
当n=﹣1时，点P与点A重合，不符合题意舍去．
∴点P的坐标为（ ， 
）
（3）
解：∵y=﹣x2+x+2，=﹣（x﹣ ）2+ ，
∴M（ ， ）．
如图所示，连结AM交直线DE与点G，连结CG、CM此时，△CMG的周长最小．
设直线AM的函数解析式为y=kx+b，且过A（﹣1，0），M（ ， ）．
根据题意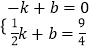得： 
，解得 
．
∴直线AM的函数解析式为y= 
+ ．
∵D为AC的中点，
∴D（﹣ ，1）．
设直线AC的解析式为y=kx+2，将点A的坐标代入得：﹣k+2=0，解得k=2，
∴AC的解析式为y=2x+2．
设直线DE的解析式为y=﹣ x+c，将点D的坐标代入得： 
+c=1，解得c= 
，
∴直线DE的解析式为y=﹣ x+ ．
将y=﹣ x+ 与y= + 联立，解得：x=﹣ 
，y= 
．
∴在直线DE上存在一点G，使△CMG的周长最小，此时G（﹣ ， ）
【解析】（1）将点A和点B的坐标代入抛物线的解析式得到关于b、c的方程组，然后求得a，b的值，从而得到问题的答案；（2）把A（﹣1，0）代入y=mx+ 求得m的值，可得到直线AQ的解析式，设点P的横坐标为n，则P（n，﹣n2+n+2），N（n， n+ ），F（n，0），
然后用含n的式子表示出PN、NF的长，然后依据PN=2NF列方程求解即可；（3）连结AM交直线DE与点G，连结CG、CM此时，△CMG的周长最小，先求得点M的坐标，然后求得AM和DE的解析式，最后在求得两直线的交点坐标即可．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
