题目内容
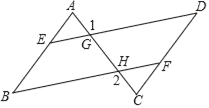
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
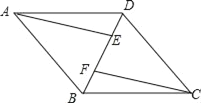
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)利用平行四边形的性质结合全等三角形的判定方法(AAS),得出即可;
(2)利用全等三角形的性质得出AE=CF,进而求出四边形AFCE是平行四边形.,再利用菱形的判定方法得出答案.
试题解析:证明:(1)如图1.
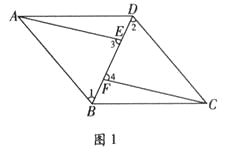
∵四边形ABCD是平行四边形,
∴AB∥DC,AB="DC."
∴∠1=∠2.
∵AE∥CF,
∴∠3=∠4.
在△AEB和△CFD中,
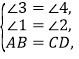
∴△AEB≌△CFD.
(2)如图2.
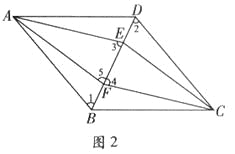
∵△AEB≌△CFD,
∴AE=CF.
∵AE∥CF,
∴四边形AFCE是平行四边形.
∵∠5=∠4,∠3=∠4,
∴∠5=∠3.
∴AF=AE.
∴四边形AFCE是菱形.

练习册系列答案
相关题目