Question

【题目】如图，已知双曲线y= 经过点B（3 ，1），点A是双曲线第三象限上的动点，过B作BC⊥y轴，垂足为C，连接AC．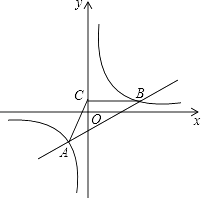
（1）求k的值；
（2）若△ABC的面积为6 ，求直线AB的解析式；
（3）在（2）的条件下，写出反比例函数值大于一次函数值时x的取值范围．

Answer 1

【答案】
（1）解：把B（3 ，1）代入y= 中得，1= ，

∴k=3

（2）解：设△ABC中BC边上的高为h，

∵BC⊥y轴，B（3 ，1）

∴BC=3 ，

∵△ABC的面积为6 ，

∴ BCh=6 ，

∴h=4，

∴点A的纵坐标为1﹣4=﹣3，

把y=﹣3代入y= ，

∴x=﹣ ，

∴A（﹣ ，﹣3），设直线AB的解析式为：y=mx+n，

把A（﹣ ，﹣3）和B（3 ，1）代入y=mx+n，

解得：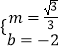

∴直线AB的解析式为y= ﹣2

（3）解：由图象可得：x＜﹣ 或0＜x＜3
【解析】（1）将B的坐标代入双曲线的解析式即可求出k的值．（2）设△ABC中BC边上的高为h，由△ABC的面积为6 可求出h的值，从而可求出A的纵坐标为﹣3，然后即可求出点A的坐标，最后将A与B的坐标代入一次函数的解析式即可求出答案．（3）找出反比例函数图象位于一次函数图象上方的部分即可求出x的范围．