题目内容
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
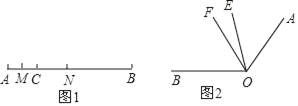
【答案】(1)MN的长为8cm;(2)∠AOB=120°.
【解析】
试题(1)直接利用两点之间距离分别得出CN,MC的长进而得出答案;
(2)直接利用角平分线的性质以及结合已知角的关系求出答案.
试题解析:解:(1)∵M是AC的中点,AC=6cm,∴MC=![]() AC=6×
AC=6×![]() =3cm.
=3cm.
又因为CN:NB=1:2,BC=15cm,∴CN=15×![]() =5cm,∴MN=MC+CN=3+5=8cm,∴MN的长为8cm;
=5cm,∴MN=MC+CN=3+5=8cm,∴MN的长为8cm;
(2)∵∠BOE=2∠AOE,∠AOB=∠BOE+∠AOE,∴∠BOE=![]() ∠AOB.
∠AOB.
∵OF平分∠AOB,∴∠BOF=![]() ∠AOB,∴∠EOF=∠BOE﹣∠BOF=
∠AOB,∴∠EOF=∠BOE﹣∠BOF=![]() ∠AOF.
∠AOF.
∵∠EOF=20°,∴∠AOB=120°.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
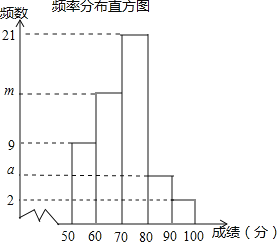
【题目】为参加全区的“我爱古诗词”知识竞赛,王晓所在学校组织了一次古诗词知识测试![]() 王晓从全体学生中随机抽取部分同学的分数
王晓从全体学生中随机抽取部分同学的分数![]() 得分取正整数,满分为100分
得分取正整数,满分为100分![]() 进行统计
进行统计![]() 以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图
以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图![]() 请根据以上频率分布表和布直方图,回答下列问题:
请根据以上频率分布表和布直方图,回答下列问题:
组别 | 分组 | 频数 | 频率 |
1 |
| 9 |
|
2 |
| m | b |
3 |
| 21 |
|
4 |
| a |
|
5 |
| 2 | n |
(1)分别求出a、b、m、n的值;![]() 写出计算过程
写出计算过程![]()
(2)老师说:“王晓的测试成绩是被抽取的同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)得分在![]() 的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?