题目内容
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】分析:由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠CBM=∠MDO,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.
详解:①∵四边形ABCD和EFGC都为正方形,
∴CB=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.
在△BCE和△DCG中,CB=CD,∠BCE=∠DCG,CE=CG,
∴△BCE≌△DCG,
∴BE=DG,
故结论①正确.
②如图所示,设BE交DC于点M,交DG于点O.
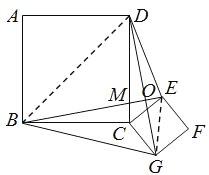
由①可知,△BCE≌△DCG,
∴∠CBE=∠CDG,即∠CBM=∠MDO.
又∵∠BMC=∠DMO,∠MCB=180°-∠CBM-∠BMC,∠DOM=180°-∠CDG-∠MDO,
∴∠DOM=∠MCB=90°,
∴BE⊥DG.
故②结论正确.
③如图所示,连接BD、EG,
由②知,BE⊥DG,
则在Rt△ODE中,DE2=OD2+OE2,
在Rt△BOG中,BG2=OG2+OB2,
在Rt△OBD中,BD2=OD2+OB2,
在Rt△OEG中,EG2=OE2+OG2,
∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.
在Rt△BCD中,BD2=BC2+CD2=2a2,
在Rt△CEG中,EG2=CG2+CE2=2b2,
∴BG2+DE2=2a2+2b2.
故③结论正确.
故选:D.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: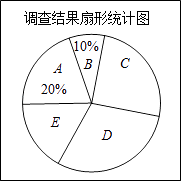
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?