题目内容
【题目】已知x2﹣8x+16﹣m2=0(m≠0)是关于x的一元二次方程
(1)证明:此方程总有两个不相等的实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c是该方程的两个实数根,求△ABC的面积.
【答案】(1)证明见解析;(2)△ABC的面积为![]() .
.
【解析】
(1)计算判别式的值得到△=4m2,从而得到△>0,然后根据判别式的意义得到结论;
(2)利用求根公式解方程得到x=4±m,即b=4+m,c=4﹣m,讨论:当b=a=6时,即4+m=6,解得m=2,利用勾股定理计算出底边上的高,然后计算△ABC的面积;当c=a时,即4﹣m=6,解得m=﹣2,即a=c=6,b=2,利用同样方法计算△ABC的面积.
(1)证明:△=(﹣8)2﹣4×(16﹣m2)
=4m2,
∵m≠0,
∴m2>0,
∴△>0,
∴此方程总有两个不相等的实数根;
(2)解:∵![]()
∴![]() ,
,
即b=4+m,c=4﹣m,
∵m≠0
∴b≠c
当b=a时,4+m=6,解得m=2,即a=b=6,c=2,
如图,AB=AC=6,BC=2,AD为高,
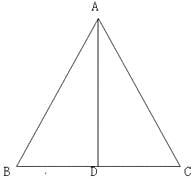
则BD=CD=1,
∴![]()
∴△ABC的面积为:![]() ×2×
×2×![]() =
=![]() ;
;
当c=a时,4﹣m=6,解得m=﹣2,即a=c=6,b=2,
如图,AB=AC=6,BC=2,AD为高,

则BD=CD=1,
∴![]()
∴△ABC的面积为:![]() ×2×
×2×![]() =
=![]() ,
,
即△ABC的面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目