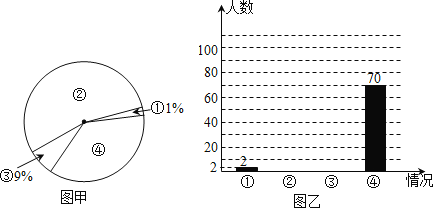
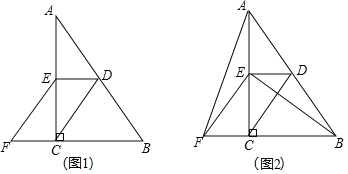
题目内容
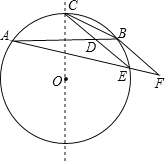
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线;以BC为直径的⊙O交BD于点E,连接CE并延长交AB于点F,连接DF,
(1)补全图中图形;(要求:清晰、准确,标出相应字母,不写作法,不必保留作图痕迹)
(2)DC=DF;
(3)若AC=8,BC=6,求CF的长.
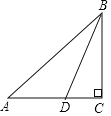
【答案】(1)作图见解析;(2)证明见解析;(3)CF![]() .
.
【解析】
(1)由题意画出图形;
(2)通过证明△BEF≌△BEC,可得EF=CE,可得BD是CF的垂直平分线,即DF=CD;
(3)由勾股定理可求AB的长,CD的长,BD的长,由三角形面积公式可求CE的长,即可求CF的长.
(1)如图,
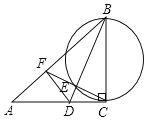
(2)∵BC是直径,
∴∠CEB=90°.
∵BD平分∠CBF,
∴∠FBD=∠CBD,且BD=BD,∠CEB=∠BEF=90°,
∴△BEF≌△BEC(ASA),
∴EF=CE,且BD⊥CF,
∴BD是CF的垂直平分线,
∴DF=CD
(3)∵AC=8,BC=6,
∴AB![]()
![]() 10.
10.
∵△BEF≌△BEC,
∴BF=BC=6,
∴AF=4,
∵BD是CF的垂直平分线,即点C、点F关于直线BD对称,
∴∠BFD=∠BCD=90°,
∴∠AFD=90°,
在Rt△AFD中,AD2=AF2+DF2,
∴(8﹣CD)2=16+CD2,
∴CD=3,
∴BD![]()
![]() 3
3![]()
∵S△BCD![]() BC×CD
BC×CD![]() BD×CE,
BD×CE,
∴3×6=3![]() CE,
CE,
∴CE![]() ,
,
∴CF=2CE![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目