��Ŀ����
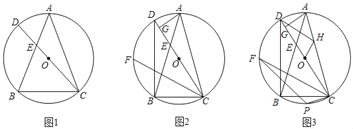
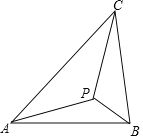
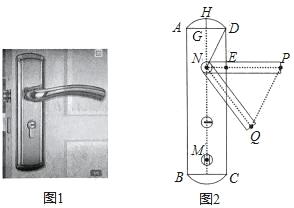
����Ŀ��С���ҵ��ſ���װ��һ�ѷ�����������ͼ1������ƽ��ṹͼ��ͼ2��ʾ���������Կ����������Ȼ�AD����BC�;���ABCD��ɣ���BC��Բ���ǵ�����ť��M����֪��AD�Ĺ��θ�GH��2cm��AD��8cm��EP��11cm��������PN���ŵ�N��ת��NQλ��ʱ����������ʱֱ��PQ�뻡BC���ڵ�Բ���У���PQ��DN��tan��NQP��2��
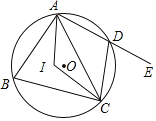
��1����BC����Բ�İ뾶Ϊ_____cm��
��2���߶�AB�ij���ԼΪ_____cm����![]() ��2.236�������ȷ��0.1cm��
��2.236�������ȷ��0.1cm��
���𰸡�5 29.8
��������
��1����ͼ������BM����HM��BC��K���ӳ�PQ��NM���ӳ����ڵ�T����ֱ��PQ�뻡BC���ڵ�Բ������J������MJ����Rt��BMK�����ù��ɶ�����һ�����ɣ�
��2����������ɽ�һ���ó�tan��DNE��tan��NQP��2��![]() ���Ӷ��ó�NP�ij������������tan��TMJ��tan��NPT��һ����⣬ͨ��GN+MN+MK���AB�ij�����.
���Ӷ��ó�NP�ij������������tan��TMJ��tan��NPT��һ����⣬ͨ��GN+MN+MK���AB�ij�����.
��ͼ������BM����HM��BC��K���ӳ�PQ��NM���ӳ����ڵ�T����ֱ��PQ�뻡BC���ڵ�Բ������J������MJ��

��BM��r����Rt��BMK������r2��42+��r��2��2��
���r��5��
��BM��5������BC����Բ�İ뾶Ϊ5cm��
��2����DN��PB��
���DNE����P��
��NP��NQ��
���P����NQP��
���DNE����NQP��
��tan��DNE��tan��NQP��2��![]() ��
��
��NE��DG��4��
��DE��NG��8��
��NP��NE+EP��4+11��15��
��ֱ��PQ�뻡BC���ڵ�Բ������J��
��MJ��PQ��MJ��5��
���TMJ����NPT��
��tan��TMJ��tan��NPT��2��
��![]() ��
��
��NT��15��2��30��TJ��5��2��10��
��MT=![]() ,
,
��MN��NT��MT��30��5![]() ��
��
��AB��GN+MN+MK��8+30��5![]() +3��41��5
+3��41��5![]() ��29.8cm
��29.8cm
�ʴ�Ϊ����1��5����2��29.8��

 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�