题目内容
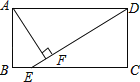
【题目】如图，正方形ABCD的边长为定值，E是边CD上的动点（不与点C，D重合），AE交对角线BD于点F，FG⊥AE交BC于点G，GH⊥BD于点H．现给出下列命题：①AF＝FG；②FH的长度为定值．则（ ）
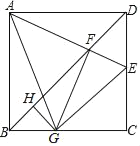
A.①是真命题，②是真命题B.①是真命题，②是假命题
C.①是假命题，②是真命题D.①是假命题，②是假命题
【答案】A
【解析】
先根据正方形的性质、三角形全等判定定理与性质得出
，再根据四边形的内角和定理、邻补角定义、等量代换得出
，然后根据等腰三角形的性质得出
，从而得出
，即可判断①正确；先根据直角三角形的性质得出
，再结合题（1）的结论，根据三角形的判定定理与性质可得
，然后根据正方形ABCD的边长为定值即可判断②正确．
（1）证明：连接CF
在正方形ABCD中，
在△ABF和△CBF中，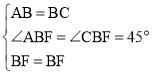
∴在四边形ABGF中，
又
；
（2）连接AC交BD于O
∵四边形ABCD是正方形，
由（1）知，
正方形ABCD的边长为定值
正方形ABCD的对角线AC也为定值，从而
为定值
的长度为定值
综上，①②正确
故选：A．
名校课堂系列答案
【题目】为积极响应“弘扬传统文化”的号召，某学校组织全校1200名学生进行经典诗词诵读活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取40名学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图如图所示.
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表如下：
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
（1）求活动启动之初学生“一周诗词诵背数量”的中位数；
（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；
（3）选择适当的统计量，至少从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果.
