题目内容
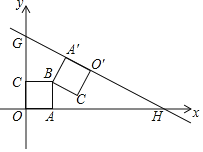
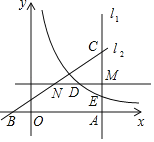
【题目】如图,直线l1经过点A(6,0),且垂直于x轴,直线l2:y=kx+b(b>0)经过点B(﹣2,0),与l1交于点C,S△ABC=16.点M是线段AC上一点,直线MN∥x轴,交l2于点N,D是MN的中点.双曲线y=![]() (x>0)经过点D,与l1交于点E.
(x>0)经过点D,与l1交于点E.
(1)求l2的解析式;
(2)当点M是AC中点时,求点E的坐标;
(3)当MD=1时,求m的值.
【答案】(1)y=![]() x+1;(2)E(6,
x+1;(2)E(6,![]() );(3)15.
);(3)15.
【解析】
(1)根据三角形面积公式求得C点的坐标,然后根据待定系数法即可求得直线l2的解析式;
(2)根据题意求得M点的坐标,进而求得N点的坐标,即可求得D点的坐标,根据待定系数法即可求得m的值;
(3)设M(6,n),当MD=1时,则D(5,n),N(4,n),把N(4,n)代入直线l2求得n的值,从而得到D的坐标,根据待定系数法即可求得m的值.
(1)∵点A(6,0),点B(﹣2,0),
∴AB=8,
∵S△ABC=![]() ABAC=16,
ABAC=16,
∴AC=4,
∴C(6,4),
∵直线l2:y=kx+b(b>0)经过点B(﹣2,0),与l1交于点C,
∴![]() ,解得:
,解得:![]() ,
,
∴直线l2的解析式为:y=![]() x+1;
x+1;
(2)∵点M是AC中点,
∴M(6,2),
把y=2代入直线l2:y=![]() x+1得:2=
x+1得:2=![]() x+1,
x+1,
解得:x=2,
∴N(2,2),
∵D是MN的中点.
∴D(4,2),
∵双曲线y=![]() (x>0)经过点D,
(x>0)经过点D,
∴m=4×2=8,
∴双曲线为:y=![]() ,
,
把x=6代入得y=![]() ,
,
∴E(6,![]() );
);
(3)设M(6,n),当MD=1时,则D(5,n),N(4,n),
把N(4,n)代入直线l2:y=![]() x+1得n=
x+1得n=![]() =3,
=3,
∴D(5,3),
∵双曲线y=![]() (x>0)经过点D,
(x>0)经过点D,
∴m=5×3=15.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.