题目内容
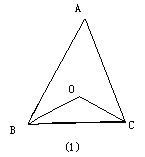
(1)如图(1),在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数。
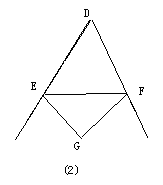
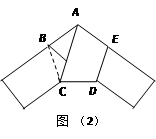
(2)如图(2),△DEF两个外角的平分线相交于点G,∠D=40°,求∠EGF的度数。
(3)由(1)、(2)可以发现∠BOC与∠EGF有怎样的数量关系?
设∠A=∠D=n°,∠BOC与∠EGF是否还具有这样的数量关系?
为什么?

(2)如图(2),△DEF两个外角的平分线相交于点G,∠D=40°,求∠EGF的度数。

(3)由(1)、(2)可以发现∠BOC与∠EGF有怎样的数量关系?
设∠A=∠D=n°,∠BOC与∠EGF是否还具有这样的数量关系?
为什么?
(1)110° (2)70° (3)互补
试题分析:(1)∠BOC=180°-∠OBC-∠OCB=180°-
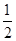 ∠ABC-
∠ABC-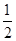 ∠ACB=180°-
∠ACB=180°-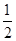 (180°-∠A)=110°。
(180°-∠A)=110°。(2)△DEF两个外角和=2∠D+∠EDF+∠DFE=180°+∠D=220°。
所以∠G=180°-∠FEG-∠EFG=180°-
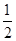 △DEF两个外角和=70°。
△DEF两个外角和=70°。(3)由(1)、(2)可以发现∠BOC与∠EGF互补
设∠A=∠D=n°∠BOC与∠EGF依旧互补。
点评:本题难度中等,主要考查学生对三角形性质和探究规律解决几何问题的能力。为中考常见题型,学生要牢固掌握解题技巧。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
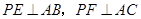 ,垂足分别为点
,垂足分别为点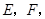
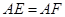 .
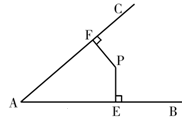
.
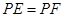 ;
;

 3,则
3,则 ___
___