题目内容
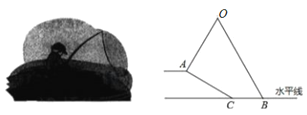
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度，将测角仪放在F处测得大树顶端A的仰角为30°，放在G处测得大树顶端A的仰角为60°，树叶部分下端B的仰角为45°，已知点F、G与大树底部H共线，点F、G相距15米，测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB．
【答案】AH的高度是(
)米，AB的高度是
米.
【解析】
设CD＝x米,可得AC＝
，因为Rt△ACE，所以EC＝3x，然后求出x的值，可以得到AC,AH的值，最后根据Rt△BCD，得出AB的值.
解：由题意可知∠AEC＝30°，∠ADC＝60°，∠BDC＝45°，FG＝15.
设CD＝x米，则在Rt△ACD中，由 
得AC＝.
又Rt△ACE中，由
得EC＝3x.
∴3x＝15＋x.
∴x＝7.5.
∴AC＝
.∴AH＝
.
∵在Rt△BCD中，∠BDC＝45°，∴BC＝DC＝7.5.∴AB＝AC﹣BC＝
．
答：AH的高度是()米，AB的高度是米.
练习册系列答案
相关题目
