题目内容
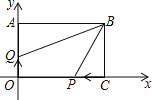
【题目】如图，已知直线AC的表达式为y＝
x＋8，点P从点A开始沿AO向点O以1个单位/s的速度移动，点Q从点O开始沿OC向点C以2个单位/s的速度移动．如果P，Q两点分别从点A，O同时出发，经过几秒能使△PQO的面积为8个平方单位？
【答案】2 s或4 s
【解析】
首先求得直线与两坐标轴的交点坐标，然后表示出三角形的两边利用三角形的面积计算公式列出方程计算即可．
解：直线y＝
x＋8与x轴，y轴的交点坐标分别为A(－6，0)，C(0，8)，∴OA＝6，OC＝8.设点P，Q移动的时间为x s，根据题意得
×2x·(6－x)＝8.整理，得x2－6x＋8＝0，解得x1＝2，x2＝4.当x＝2时，AP＝2，OQ＝4，点P，Q分别在OA，OC上，符合题意；当x＝4时，AP＝4，OQ＝8，此时点Q与点C重合，同样符合题意．答：经过2 s或4 s，能使△PQO的面积为8个平方单位
练习册系列答案
相关题目
