题目内容
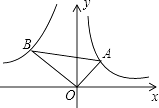
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12![]() 时,OA的长为____.
时,OA的长为____.

【答案】8
【解析】分析:
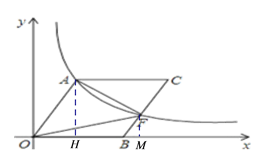
过点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,在由已知易得:AH=![]() ,OH=
,OH=![]() ,由此可得S△AOH=
,由此可得S△AOH=![]() 由点F是平行四边形AOBC的BC边上的中点,可得BF=
由点F是平行四边形AOBC的BC边上的中点,可得BF=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,由此可得S△BMF=
,由此可得S△BMF=![]() ,由S△OAF=
,由S△OAF=![]() 可得S△OBF=
可得S△OBF=![]() ,由此可得S△OMF=
,由此可得S△OMF=![]() ,由点A、F都在反比例函数
,由点A、F都在反比例函数![]() 的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
详解:
如下图,点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,
∵四边形AOBC是平行四边形,∠AOB=60°,点F是BC的中点,S△OAF=![]() ,
,
∴AH=![]() ,OH=
,OH=![]() ,BF=
,BF=![]() ,∠FBM=60°,S△OBF=
,∠FBM=60°,S△OBF=![]() ,
,
∴S△AOH=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,
,
∴S△BMF=![]() ,
,
∴S△OMF=![]() ,
,
∵由点A、F都在反比例函数![]() 的图象上,
的图象上,
∴S△AOH=S△BMF,
∴![]() =
=![]() ,
,
化简得:![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴OA=8.
故答案为:![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】观察下列一组勾股数:
|
|
| |
第1组 | 3=2×1+1 | 4=2×1×(1+1) | 5=2×1×(1+1)+1 |
第2组 | 5=2×2+1 | 12=2×2×(2+1) | 13=2×2×(2+1)+1 |
第3组 | 7=2×3+1 | 24=2×3×(3+1) | 25=2×3×(3+1)+1 |
第4组 | 9=2×4+1 | 40=2×4×(4+1) | 41=2×4×(4+1)+1 |
… | … | … | … |
观察以上各组勾股数的特点:
(1)请写出第7组勾股数![]() ,
,![]() ,
,![]() ;
;
(2)写出第![]() 组勾股数
组勾股数![]() ,
,,
![]() .
.