题目内容
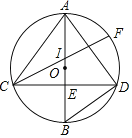
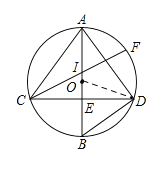
【题目】如图,⊙O中直径AB⊥弦CD于E,点F是![]() 的中点,CF交AB于I,连接BD、AC、AD.
的中点,CF交AB于I,连接BD、AC、AD.
(1)求证:BI=BD;
(2)若OI=1,OE=2,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径是3+![]()
【解析】
(1)利用三角形内心的性质及外角的性质可得∠BID=∠BDI,从而可证BI=BD;
(2)设⊙O的半径为r,根据勾股定理列方程得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,解方程可得结论.
(1)证明:如图,连接DI,
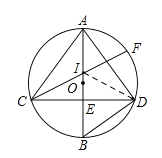
∵AB为⊙O的直径,且AB⊥CD,
∴![]() ,
,
∴∠CAB=∠BAD,∠BAD=∠BDC,
∵点F是![]() 的中点,
的中点,
∴∠ACF=∠DCF,
∴I是△ADC的内心,
∴∠ADI=∠CDI,
∵∠BID=∠BAD+∠ADI,∠BDI=∠BDC+∠CDI,
∴∠BID=∠BDI,
∴BI=BD;
(2)连接OD,
设⊙O的半径为r,
∵OI=1,OE=2,
∴BE=r﹣2,BD=BI=r+1,
由勾股定理得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,
r2﹣6r﹣1=0,
r1=3+![]() ,r2=3-
,r2=3-![]() (舍),
(舍),
答:⊙O的半径是3+![]() .
.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目