题目内容
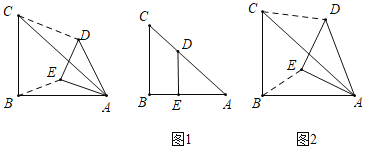
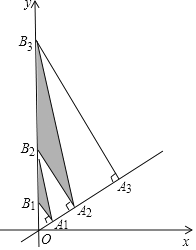
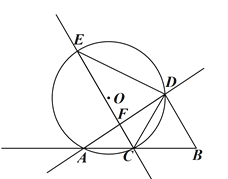
【题目】如图,AB=4,C为射线BA上一动点,以BC为边向上作正三角形BCD,⊙O过A、C、D三点,E为⊙O上一点,满足AD=ED,直线CE交直线AD于F.
(1)求证:CE∥BD;
(2)设CF=a,若C在线段AB上运动.
①求点E运动的路径长;
②求a的范围;
(3)若AC=1,求 tan∠DEC.
【答案】(1)证明见解析;(2)①4;②0≤a≤1;(3)![]() 或
或![]() ;
;
【解析】
(1)连接AE,证△ADE为等边三角形即可得到∠ECD=∠CDB=60°,则有CE∥BD.
(2) ①首先分析E点的运动轨迹是在于AB平行且距离为2![]() 的直线上,再进行计算;
的直线上,再进行计算;
②设CB的长为x(0<x<4),通过证明![]() ,得到用含x的式子表示a,从而求出a的取值范围.
,得到用含x的式子表示a,从而求出a的取值范围.
(3)分两种情况讨论:点C在线段AB上和在A点的左边两种情况分别进行计算求解.
解:(1)连接AE

∵三角形BCD是等边三角形,
∴∠B=∠BCD=∠BDC=60°.
∵四边形ACDE是圆O的内接四边形,
∴∠AED+∠ACD=180°.
又∵∠ACD+∠BCD=180°,
∴∠AED=∠BCD=60°.
∵AD=AE,
∴三角形ADE是等边三角形.
∴∠EAD=60°,
∴∠EAD=∠ECD=∠CDB=60°.
∴CE∥BD;
(2) ①∵∠EDA=∠CDB=60°,
∴∠EDA+∠ADC=∠CDB+∠ADC,即∠EDC=∠ADB.
又∵ED=AD,CD=DB,
∴![]() .
.
∴EC=AB=4.
过点E作EG⊥AB于点G,在直角三角形CFE中,∠ECA=60°,∴EG=![]() EC=2
EC=2![]()
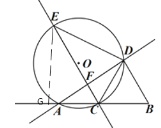
∴点E的运动轨迹为于AB平行且距离为2![]() 的直线上.
的直线上.
所以点C在A时,得到点E1, 点C在B时,得到点E2,∴四边形E1ACE2是平行四边形,
所以E1E2=AB=4.
∴E的运动路径长为4.
②设CB的长为x(0<x<4),则AC=4-x,BD=CB=x.
∵CE∥BD,
∴![]()
∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
∴a=-![]() +x=-
+x=-![]() (x-2)2+1.
(x-2)2+1.
当x=2时,a有最大值为1;
当x=0时,a有最小值0.
∴0≤a≤1.
(3)当C在AB之间时,过点D作DH⊥AB与点H,则AC=1,BC=BD=3.
∴BH=![]() BC=
BC=![]() ,DH=
,DH=![]() BD=
BD=![]() .
.
∴AH=AB-BH=![]() .
.
∴tan∠DEC=tan∠DAH=![]() =
=![]() .
.
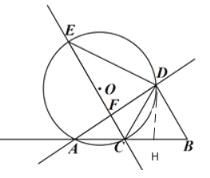
当C在A的左边时,同理可以求得tan∠DEC=tan∠DAH=![]() .
.
∴tan∠DEC的值为![]() 或
或![]() ;
;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案