��Ŀ����
����Ŀ��ijУ��һ�δ�μ��У����������ӻ��ʽ��A���ܲ���B��������C�����٣�D����Ϸ.ȫУѧ����ѡ����һ����ʽ������С�ܶ�ͬѧ��ѡ�õĻ��ʽ����������������飬���ݵ���ͳ�ƽ���������˲�������ͳ��ͼ.
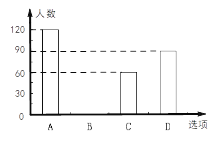
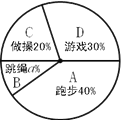
����ͳ��ͼ���ش��������⣺
��1�����ε���ѧ���� �ˣ� ![]() = ����������ͼ����������
= ����������ͼ����������
��2�������У��ѧ��2000�ˣ�������Ƹ�Уѡ�����ܲ������ֻ��ѧ��Լ�ж����ˣ�
��3��ѧУ��ÿ����A��B��C��D���ӻ��ʽ�У������ȡ���ֿ�չ���������״ͼ���б��ķ�������ÿ���ȡ��������ʽǡ�������ܲ��������������ĸ���.
���𰸡���1��300,10����ȫ����ͼ��������
��2����Уѡ���ܲ������ֻ��ѧ��Լ��800�ˣ�
��3������״ͼ��������ÿ���ȡ��������ʽǡ���ǡ��ܲ����͡��������ĸ���Ϊ![]() .
.
���������������������Ģ��ʸ�����֪������ͼ�л���������ٶ�Ӧ����ͼ����Ӧ�İٷֱȣ������������ε�������������ڴ˻��������![]() ��ֵ.����Ģ��������ġ��ܲ����İٷֱ�����Ϊ�����С��ܲ����İٷֱȣ��Դ˿��Լ������Уѡ���ܲ������ֻ��ѧ��������.����Ģ������������Żء���������ɲ�ȡ�оٷ��еĻ���״ͼ����������ע��ǡ���ǡ��ܲ����͡���������������Ӷ��������.
��ֵ.����Ģ��������ġ��ܲ����İٷֱ�����Ϊ�����С��ܲ����İٷֱȣ��Դ˿��Լ������Уѡ���ܲ������ֻ��ѧ��������.����Ģ������������Żء���������ɲ�ȡ�оٷ��еĻ���״ͼ����������ע��ǡ���ǡ��ܲ����͡���������������Ӷ��������.
�����������1����������ͼ������ͼ��֪���ܲ���������120�ˣ��ڱ������������ռ�İٷֱ�Ϊ40%��������α����������Ϊ![]() ���ˣ���
���ˣ���
������������ ![]()
![]() ���ˣ�������
���ˣ�������![]() ������
������![]() .
.
�ʷֱ�Ӧ�300��![]() ����ȫ������ͼ���£�
����ȫ������ͼ���£�
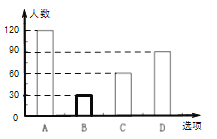
��2�������С��ܲ���������ռ������������İٷֱ�Ϊ40%�������������С��ܲ���������Ҳռ40%�����Թ��Ƹ�Уѡ���ܲ������ֻ��ѧ��Լ��![]() ���ˣ�.
���ˣ�.
��3������״ͼΪ��
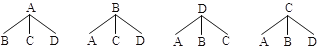
����״ͼ��֪��ÿ���ȡ��������ʽǡ���ǡ��ܲ����͡��������ĸ���![]() .
.

����Ŀ�������¼���ǽ��걦Ӧ�붬�����������ܵ�ƽ�����£�������ƽ��������͵��ǣ�������
��¼�ܴ� | ��һ�� | �ڶ��� | ������ | ������ |
ƽ������ | 3�� | 0�� | -5�� | -2�� |
A. ��һ��B. �ڶ���C. ������D. ������